
マレー・ゲルマンの論文
八道説:
強い相互作用対称性の理論
マレー・ゲルマン
1961年3月15日
加速器研究所
カリフォルニア工学研究所
=== 省略 ===
簡単な説明の為に、レプトンのユニタリー対称の論議を始める、しかし、我々の理論はバリオンとメソンと強い相互作用に関連する。ここで数学的目的の為に考える粒子は、レプトンと共にある必要はないが、示唆に富む対応物がある。我々は、3つのレプトン、ν、e-、μ-とそれらの反粒子を考える。
ニュートリノは同じ立脚地で別の二つとして扱われる、しかしながら、経験は、もし、それが4元ディラック場として扱われるならば、二つの成分は力学相互作用を持つだろうことを示唆する。(さらに、二つのニュートリノ、一つは電子とペアで別のはミューオンと)
我々が知る限り、電子的と弱い相互作用はνから区別されるe-とμ-の間で絶対的に対称的である。荷電粒子e-とμ-神秘的なそれらの質量差により分離される。これらの違いは必ずしも、どんな相互作用に対しても帰するとはしないが、どんな方法でもそれを説明できない。(もし、それを相互作用と接続することに固執するならば、重要となるただ大変な高エネルギーの組み合わせを熟考しなければならないし、その時に、それはただ学問的な興味でしかない。)しかしながら、割れるようなμーe質量は、バリオンとメソンのユニタリー対称を壊し、超多重項を同位体多重項に分離する等しく神秘的な機構に関係していることを推測する。この実施的な目的の為に、全部で三つの分離点を関係する粒子の機械的質量に置く。
現在の電子力学的量子力学において、電磁気学効果上のe-ν質量差を説明することは誰も成功していないことは良く知られている。偏見なしでその物理学的起源の問題について、質量差が電子荷と共にひねり出されるとするならば、我々の議論を進めても良いだろう。
もし、今μ-e質量差、電磁気学と弱い相互作用を切り替え消せたならば、非静止質量と知られていない組みの三つの正確な類似ディラック粒子の物理学的真空理論から去れる。この真空モデルは数学的な目的の為には理想的である、しかしながら、それは物理学的に強い相互作用粒子により動機付けられる、なぜならば、それは我々が基礎的バリオン質量とバリオンとメソン間の強い相互作用として導入した総合ユニタリー対称性の対応段階であるからである。
もちろん、対称モデルは、全ての変換下で、状態ν、e-、とμ-で不変である。
簡単さの為の最初の提案は、ただν、とe-のみを扱った場合である。
それぞれのユニタリー変換を独自に、同位相要素による両方の粒子多重から一つの、νとe-の位相要素の不変生成物から離れる(限定単一で)一つの要素に分解可能である。最初の種類の変換下での不変性は、レプトンνとe-の保存量に対応する。二つめの種類の変換の階層下で不変性から個々に、それは考慮されるだろう(数学者に2元ユニタリーユニモジュラ行列グループと呼ばれる )。
一つ目の種類の各変換は、行列e^iφ・l、lは2X2の行列、記述可能である。極小変換はl+i(δφ)lで、単位行列はこれら変換の極小生成作用素である。2番目の種類の変換は同じ方法で(三つのパウリアイソトピック・スピン行列T1,T2,T3として良いだろう)三つの独立したトーレスレス2X2の行列により生成される。こうして次式を得る。

これは2番目の種類の一般極小変換である。2番目の種類の全ての変換下での対称性はT1、T2、T3下で対称性で等しい、別の言葉で言えば独立した荷電かアイソトピック・スピン対称性である。対の片方かスピノールνとe-と二つかそれ以上のレプトンの組を変換するようなより複雑な対象の変換特性を考えることによりアイソトピック・スピン理論の完全な形式主義は、こうして、構築されることが可能である。
パウリ行列T[k]はエルミートと次式の規則に従う

今、三つ目の対象μーを含めることによりアイソトピック・スピンの考えを一般化する。再び、レプトンのユニタリー変換をこれら3X3一式の行列l(と保存レプトンに対応する)より生成されるとそれと、それら八つの独立したトレースレス3X3行列により(とユニモジュラ行列 グループから)生成されるに要素に分解する。2X2パウリ行列の類似性により典型的なこのような八つの組の行列を構築できるだろう。
それらをλ1…λ8と呼び、それらを表Iに並べる。それらはエルミーテ行列で次の特性を持つ
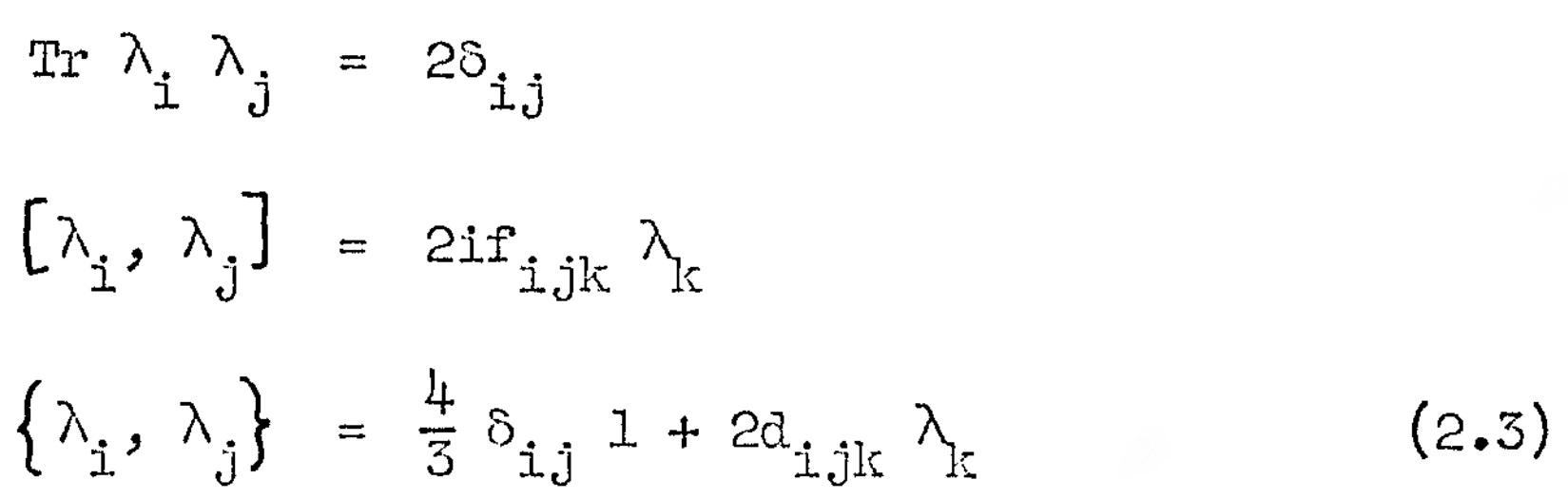
f[i,j,k]は実数で総合で式(2,2)の非対称クロネッカ記号e[i,j,k]、d[i,j,k]は実数で総合で対称性を有する。それらの特性は次式に従う。
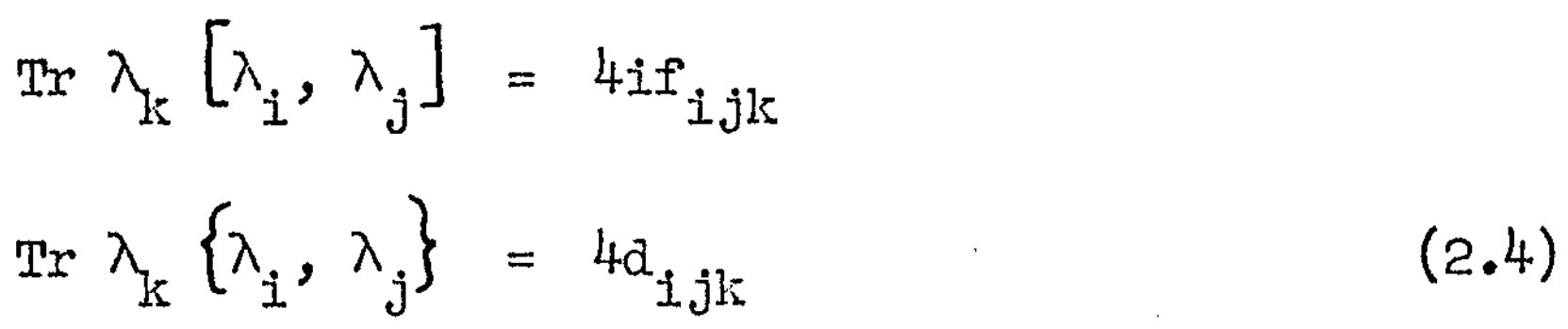
式(2,3)から得られる。
f[i,j,k]の非ゼロ要素とd[i,j,k]は我々が選んだλ[i]で表Ⅱで得られる。索引に並べられた偶と奇の置換は、それぞれの±lによるf[i,j,k]と+lによるd[i,j,k]の乗法に一致する。
2番目の種類の一般の極小変換は、もちろん

式(2,1)の類推により(2,5)となる。レプトンの保存と共に、8(番目の)λ[i]下での不変性は完全な三つのレプトンのユニタリー対称性と一致する。
===以後も同様な文と式が続くが省略する===