南部 陽一郎の論文
超電動体の類似性状の基本粒子の動的モデル .Ⅱ
南部 陽一郎
== 省略 ==
初めに、論文I中で適用された非線形スピノール場は我々の理論の基本要素ではないこと、しかし、ハイゼンベルグ理論ケースで、むしろ、我々の動的原理を探究したモデルであることを観察したい。
それにもかかわらず、我々はあるモデルを選ばなければならない。次の事実に注意する必要がある、スピン、最も軽いメソ族、は偽スカラーとアイソベクトルである、ところが、比較できる質量のそのアイソスカラー類似物は存在すると思えない。
もし、スピンが暗示的に我々の以前のモデル上の対称属性に関係していたら、これは、核粒子のモデルは、グーゼイ(Gursey)のγ5×アイソスピン・ゲージ・グループ(近似的)変動を許すだろうことをを暗示するだろう、しかし、単純なトスチェック(Touschek)γ5ゲージ・グループ下では、少なくとも、前のケースではなかったことだ。
この理由から、全体的に、次のゲージ・グループを考えることができる:
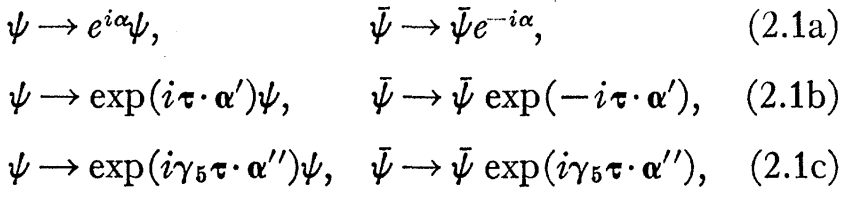
τは核子アイソスピン行列を表す。
明らかに、最初の二つは、それぞれに核子数ゲージとアイソスピン遷移である。4要素上の4次元回転グループで結合される、2番目と3番目の変換は、陽子と中性子の両方で構成される。
こうして、我々は、方程式を置き換える。(2a.1) と(2b.1)を次の変換で。
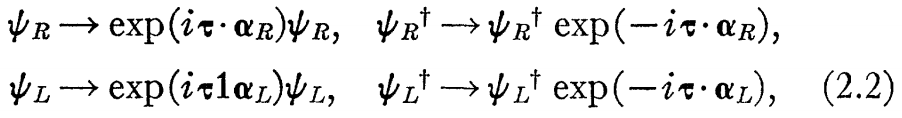
Ψ[R] とΨ[L]は右と左側の要素である。
我々の要求に一致する、最も単純なラグラジアンとして、次の式を適用する。
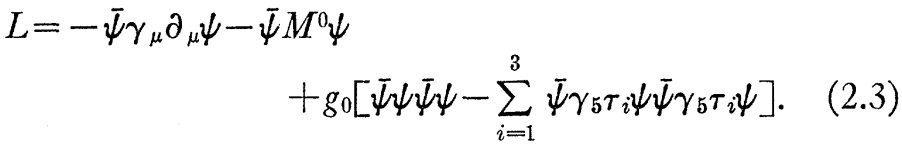
もし、裸の質量オペレータがM0=0ならば、追加式(2.1)内で、別々の“反転質量”グループ下で、このラグラジアン過程は(次式となる。)

裸の質量オペレータがM0は、グーゼイ(Gursey)グループ崩壊の可能な代理物で、有限のπ粒子の質量に関係している。運度量として、M0=0と推測して良いだろう。
質量の自己一致方程式を解く前に、(2.3)上のフィールズ(Fierz)変換の結果を与える。:相互作用は次のようになる。
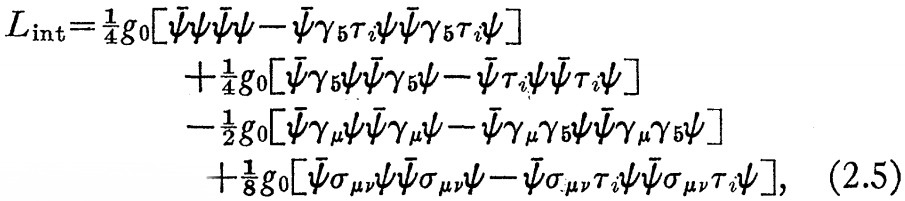
かなり、複雑な全項組合わせである。
今、Iの線形化過程を(2.3)と(2.4)に適用し、自己エネルギーを得る。
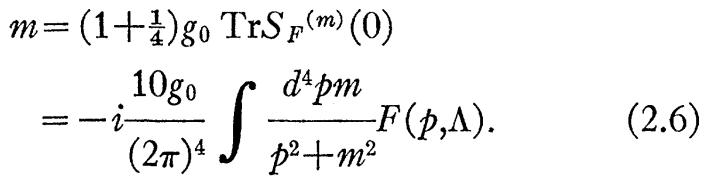
注意:トレース(作図?)はスピンとアイソスピン変数である。
これは、結合g0→5g0/2=g0’の変更により、I の(3.6)のみ異なる。そう、すなわち、以前の公式を引き継ぐことができる、平凡でない解として、もし、Iの発散整数(4.7)が使用されたならば。

式(1.1) 内の相互作用ラグラジアンと異なった結合数を含む(1.3)から、我々の簡単な近似手段により、核子と非核子ペア結合として、様々な種類の中間子を得ることを(例外として)省略する。Iで説明されたことだが、これは、ゼロ質量を持つと予想される最近の偽スカラー・中間子に関する自己エネルギー方程式に一致する固有近似である。
さらに、別形式の結合状態さえ、合理的に、存在を予想して、その性質上の妥当性を信頼できるだろう、そして、可能な結合状態の階層秩序は、基本的にスピノール間の短距離ポテンシャルと見なされる相互作用を拡張する状態である。
一般的議論として、Iの付録で与えられる次の手続きは便利である。熟考された基本方程式は、次の形式である。
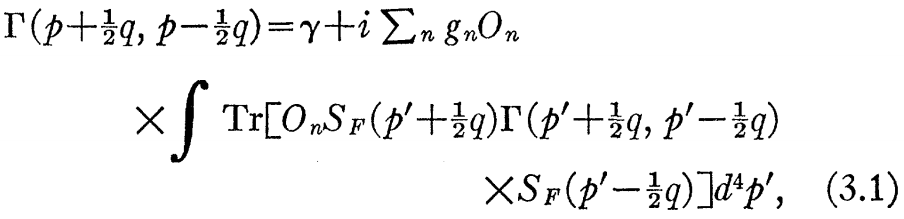
右側の加算は、相互作用ラグラジアンの様々なテンソールに関するものである。頂点関数Γ(p+(1/2)q、p-(1/2)q)は、q^2=-μ^2の値について、特有(γ=0)同種解のとき、結合状態波動関数を減ずる。簡単に、これら結合可能性がある2核子状態について議論できるだろう。
A. 偽スカラー、アイソベクトル・中間子
I 内のと異なるケース、偽スカラー相互作用~Ψγ5τiΨ(Ψ^)γ5τiΨは、ただこの状態を表す。Γi「p」=γ5τiΓ「p」を仮定すると、次式を得る。
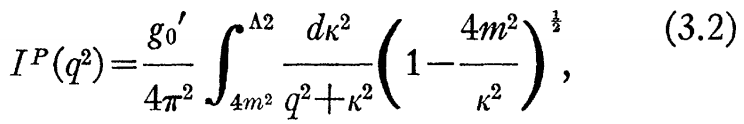
もちろん、式(2.7)が利用された。これは、ゼロ質量π粒子の一致するq^2=0の同種解である。このπ粒子-核子結合は、―Iの補遺にあるγ^P=g0’ γ5τiと非同種方程式から計算可能な―純粋偽スカラー形式である。すなわち次式を得る。
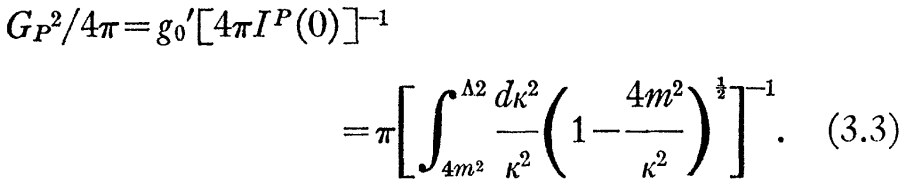
B. スカラー、アイソスカラー・中間子
Ansatz Γ=Γ^Sとして、次式を得る。
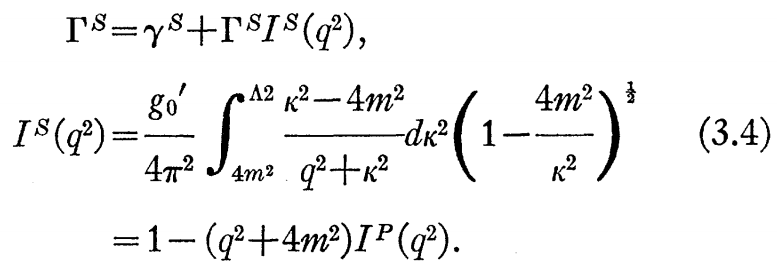
これは、ゼロ結合状態を導く:スカラー核子結合定数とq^2=-4m^2
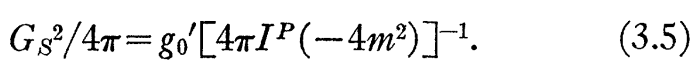
C. ベクトル・中間子
アイソスピン1と0の二つのベクトル・中間子が存在する。
アイソベクトル・中間子が、テンソール相互作用~波動関数の形式としてΨσμ「ν」τiΨ(Ψ^)σμ「ν」τiΨから得られる。
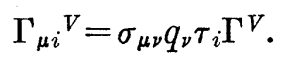
質量は、次式で決定される。
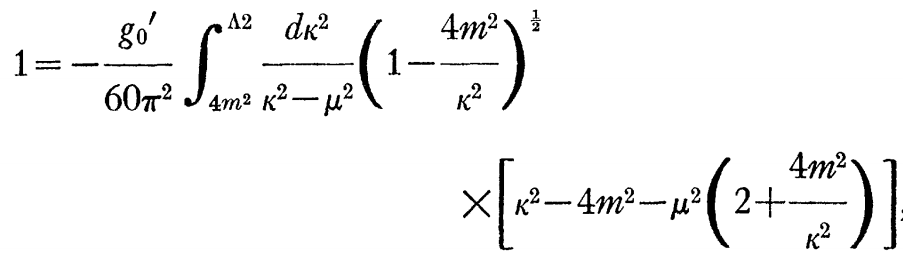
(十分に小さいΛ^2で)解がある。
![]()
この核子との中間子の結合は、必ず派生形式である。
アイソスカラー・中間子として、ベクトルとテンソル双方の相互作用は、引きよせると後者反発の公式を提供する。その波動関数は次式を持つだろう。

Γ1とΓ2の結合方程式のついて。しかしながら、この結合はかなり小さい、そして、Γ2を無視して次式を得る。
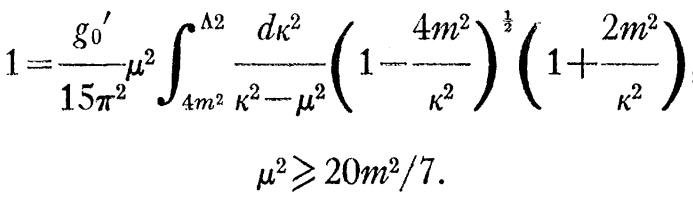
核子結合は、主として非派生的である。
D. 重陽子状態
((論文) I 中と同様に、中間子と平行して、核子-核子状態を議論可能だろう。相互作用は、手短に、次式で記述される。
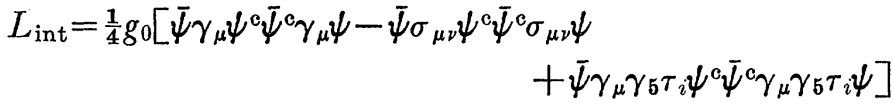
これは二つの結合状態に導くように見える:最初の二つの相互作用項から来る偽スカラー、アイソスカラー(J=1+、T=0)と最後の項から来るスカラー、アイソベクトル(J+0+、T=1)である。J=1+、T=0状態(重陽子)として、主要な主張は、誘引テンソール相互作用から来る。そして、次式を得る。
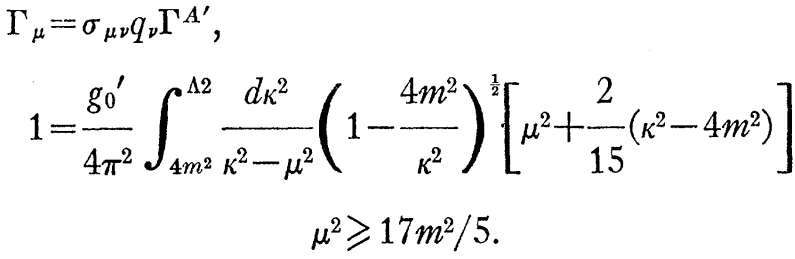
J+0+、T=1のケースでは、次式を得る。
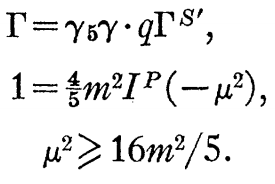
=== 以後の章は省略 ===