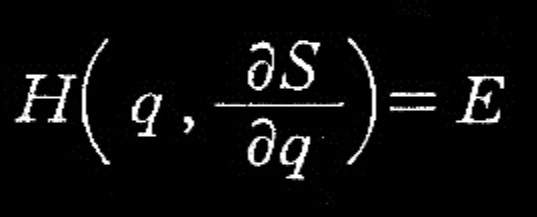
シュレディンガーの論文
固有値問題としての量子化
(第Ⅰ部)
(意訳、章のタイトルは訳者が挿入)
水素原子について自然な形で物理量が整数で表わせられることを示す。
量子化手続きは通常、ハミルトニアンの微分方程式に関係している。
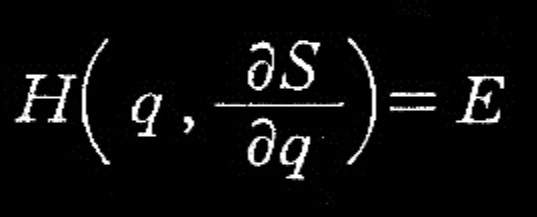
式(1)
この方程式を変数qのみで表わされる解を求める。
ここで、Sを新しい未知関数φで置き換える。φは単一の座標変数の関数で表わされるものとする。すなわち
S=Klog(φ) 式(2)
と置く。
Kは次元(物理単位)の理由から導入され、作用の次元を持つ。
これより、次式を得る。
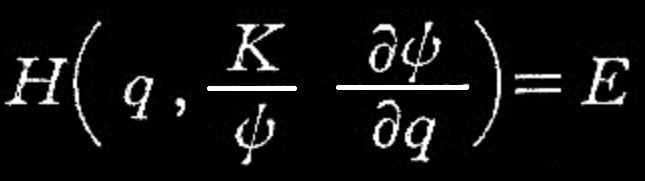
式(1)’
式(1)の解を求めず、次の要請を置く。
もし、電子の一体問題の場合、 方程式式(1)’は常にφとφの1階微分の2次形式を0にした形に変形される。実数で連続2回微分可能なφを求める。φを求める際に2次形式を全空間に渡り積分した量が停滞値をとるようにする。この変分問題のより量子化条件を置き換えよう。
初めに、Hとしてケプラー運動のハミルトニアン関数を選ぶ。直交座標でこのHを表現すると次式となる。
式(1)’’
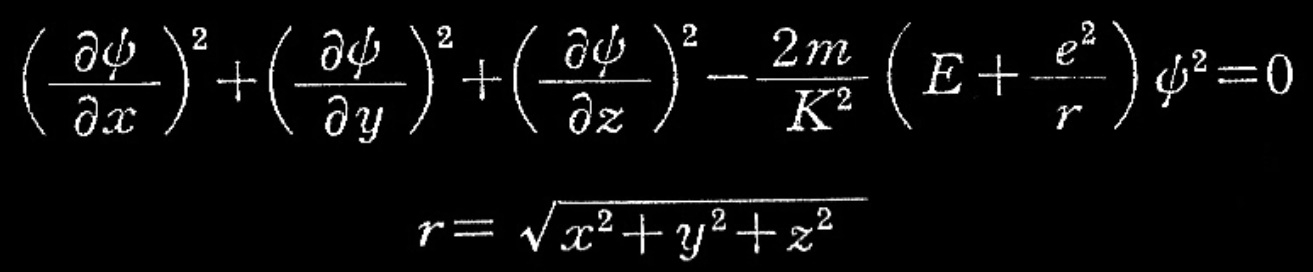
こうして変分問題は次のようになる。
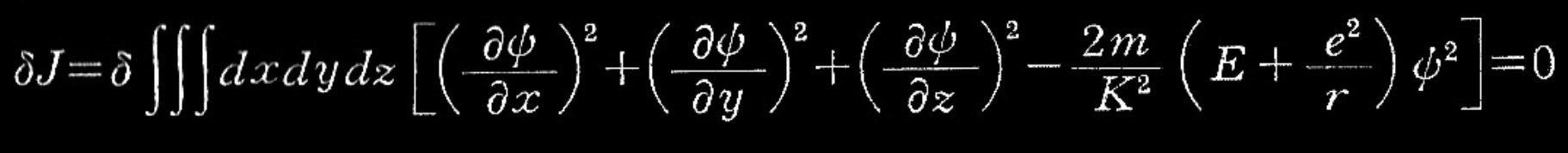
式(3)
ここで全空間にわたる。これから通常な方法により
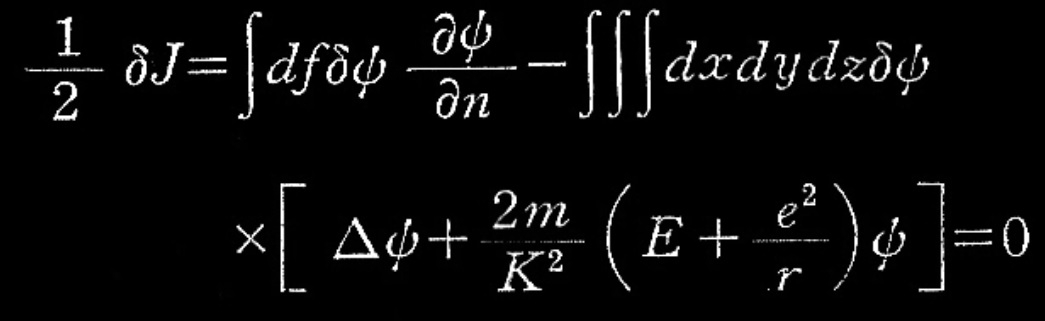
式(4)
こうして、第一に
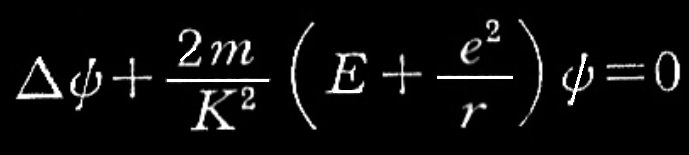
式(5)
第二に無限遠方で閉じた局面上の積分が現れる。
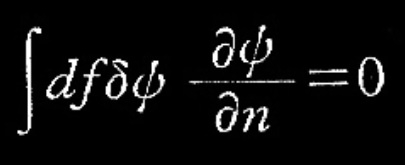
式(6)
式(5)の解は極座標r、θ、φを用いて、球面関数が現れる十分良く知られた式で表現される。rの関数部分をχ(r)とすると、次の微分方程式を得る。
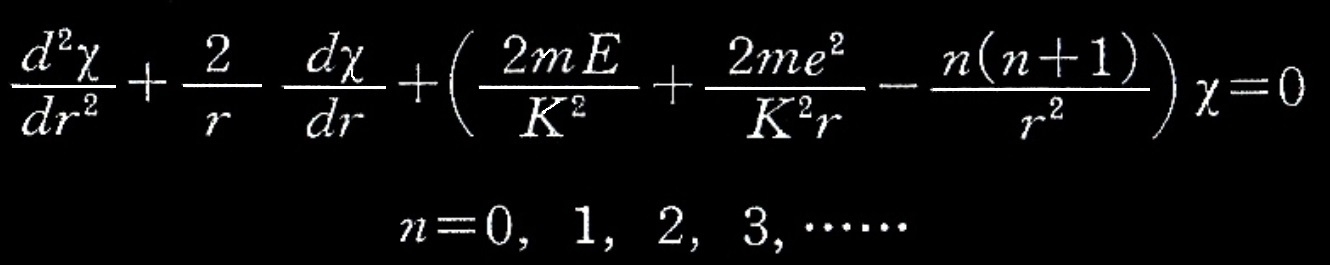
式(7)
nが整数に限定されることは、角θが1価的である為に必要であることが知られている。
===以後も根拠のないデタラメな式と主張が続くが省略する===
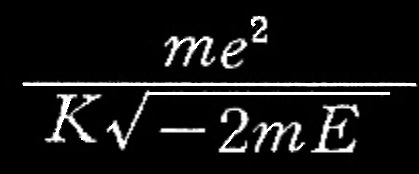
式(15)
式(15)は実数の整数である必要がある。
最初の方程式(7)の解は
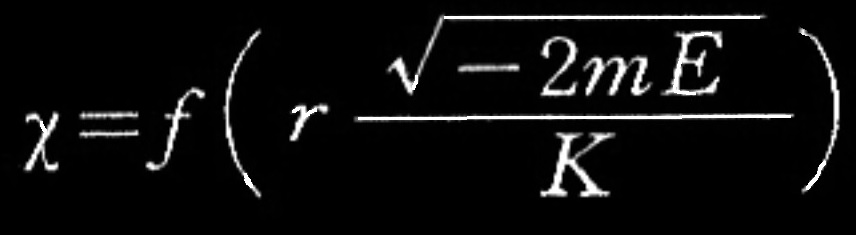
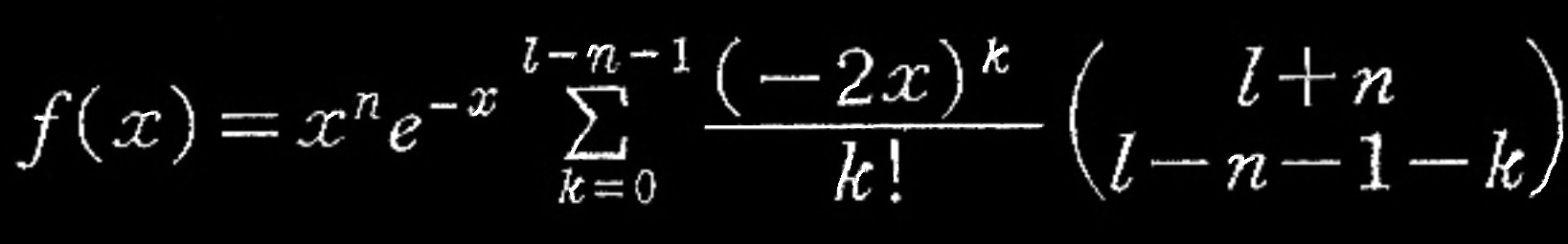
となる。
式(18)
条件(15)は次のようになる。

式(19)
これは良く知られたボーアのエネルギー準位を与え。式(2)の定数Kに次の値を与える。
K=h/2π 式(20)
lは主量子数で、nは方位量子数である。
式(18)が振動している領域の大きさは楕円の長軸と同程度である。その長さは次式となる。
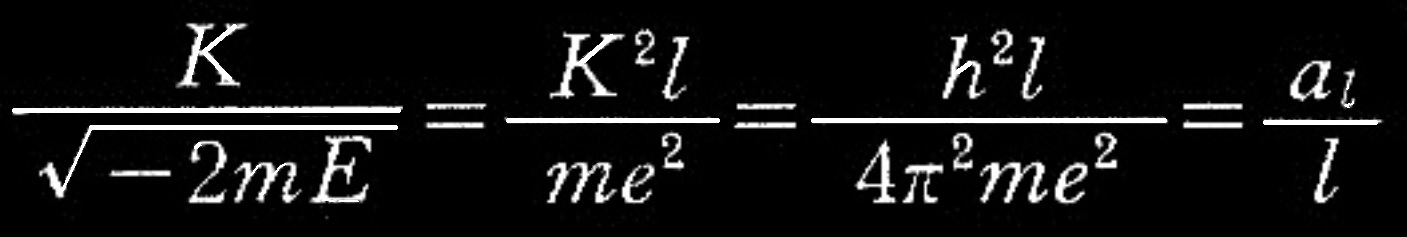
式(21)
ここでは、この式の解の精密な評価はしないが、この主張は良く確認されたものと信じる。
現在、原子内の電子軌道論が疑問視されているのに比べ、いっそう現実的になった原子内振動現象に対して、関数φを関連付けることは極めて自然と考えられる。
より複雑な場合の計算が成功するまでは、この振動現象の描像可の可能性を議論するのは止めよう。それは通常の量子論の単なる模倣に終わるかもしれない。例えば相対論的ケプラー問題は精確に計算されると半整数の部分量子が出現する。
振動現象の振動数が
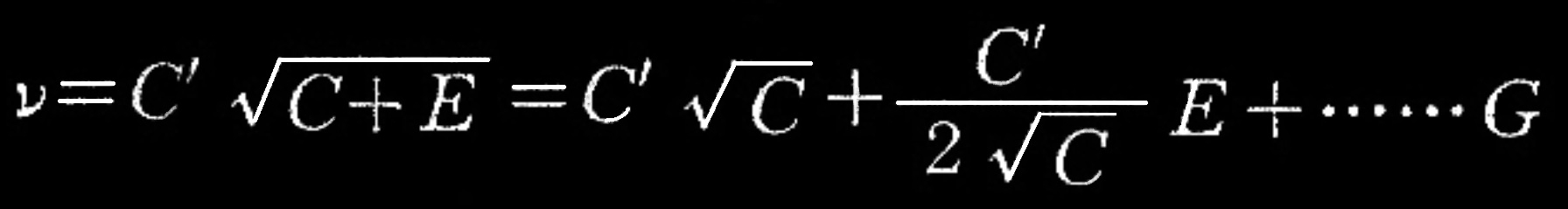
式(22)
ν:振動数 E:エネルギー C:Eよりかなり大きい定数
この式はボーアの振動条件を理解することを可能とする。
この式(22)により光子の放出などが理解可能となる。
常に、同一振動数に属する固有値は、一般に同時に刺激されると信じている。固有値の多重性は、これまでの理論の言葉で言えば縮退に対応している。