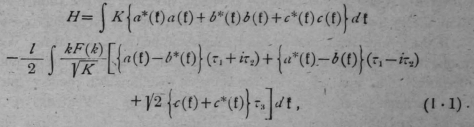
朝永 振一郎の論文
中間子と核子相互作用に於ける場の反応
朝永 振一郎
核子とメソ粒子場の相互作用は、電磁場と電子間の相互作用と、いくつかの考えで異なる。
一つめの立場として、前者の相互作用は、後者よりも激しい:前者の相互作用を特徴付ける結合定数gは、後者を特徴付ける定数eよりも、少なくとも10倍も大きい。
二つ目の立場として、核子のメソ粒子自己場ポテンシャルは、1/γ^3かσ(γ) ―より強い注目事項である 電子の自己電場、ポテンシャルは「1/r」と表わせられる―式の注目事項を持っている。
強い結合量子理論表現のケースは、場と物質の相互作用の振る舞いの明らかな画像を得ることが可能である。
我々は本論文を通して次の様に推測する、4つのポテンシャルによりメソ粒子場は描写される、そして、このようにして、メソ粒子場のベクトル理論を適用する。
我々は、単純に、二つの湯川定数g1とg2の後者は消滅すると推測する。この仮定は、ただ、縦方向の核子とメソ粒子間相互作用のみを意味する。メソ粒子のチャージに対して、我々は、対称性理論、または、簡易表現を目指した荷電理論と呼ばれるものを使用する。
我々は、核子は、それと同等な起源を持つと考える。
メソ粒子場を、(適切に正常化された)正常振動の振幅により記述しよう。このようにして、対称性理論を適用して、我々の機構上のハミルトニアン関数は次式である。
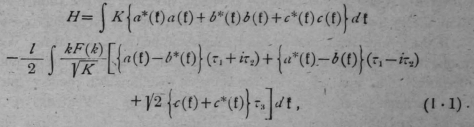
a(f)、b(f)とc(f)は、f運動量の正常振動振幅である。それらは、交換関係を満足する。
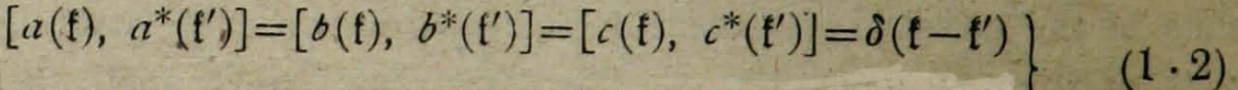
上記以外の交換子=0
もし、n+、n-、とn0を、相互作用など、場の反応として導入したならば、
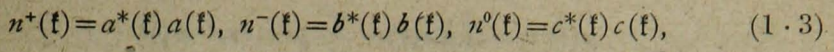
そして、n+(f)dt、n-(f)dt、とn0(f)dtは、それぞれは、ポジティブな数字、運動量が、運動量空間内fポイントで、小体積dfと置かれるところのネガティブと中性メソ粒子を意味する。
(1.1)において、自然単位系では、hとcは一体として使用される。エネルギーと同様に運動量は、1/長さの次元を持っている。
量子Kは、メソ粒子である、f運動量を持ちまた、次式で与えられる

もし、χがメソ粒子のエネルギーを示すならば
式(1,1)の中の、三つの量子τ1、τ2とτ3は、次式で次の関係を満足するアイソスピンτの三要素である。
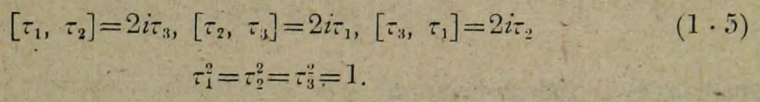
式(1,1)の中の、lは長さの次元を持つ結合定数である。そして、それは湯川のg1に次式で関係付けられる
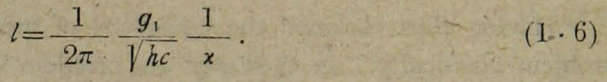
関数F(k)は、理論の破綻を避ける為に導入された、いわゆる破片(cuting off)要素である。この要素を導入した理由は、核子が有限の大きさと仮定されているからである。その粒子の半径がRで、その逆数をKで示した場合

それから、F(K)は次の固有性を持っている
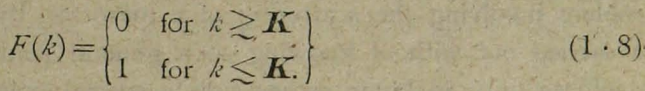
これ以後、Kを破片運動量と呼ぶ。
我々は、今、ハミルトニアン(1,1)と交換結果(1,2)と(1,5)から、通常の様式上のアイソスピン要素τ1、τ2とτ3として、振幅a、bとc運動方程式を得ることが可能である。
a、bとc、それは次式となる。
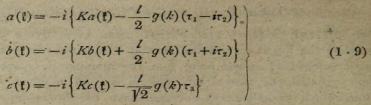
τ1、τ2とτ3として
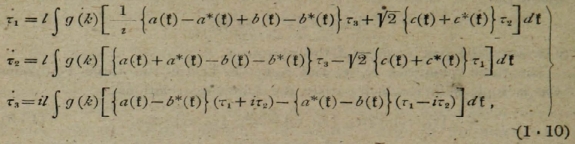
g(k)はABREVIATIONである。

この様に、得られた運動方程式、今、我々は古典論的問題を扱うことが可能である。
この方法で、我々の問題は、十分熟考後に、単純化されると同時に、相互作用の簡単な画像―、その問題に対する量子理論処置法に関して、多数の明快な理解を提供する。―を得ることが可能である。
この様にして、a、bとcは、もはやq数ではない、しかし、通常のc数である、さらに、アイソトピック スピンτは、123空間内で、通常のベクトル要素である。
しかしながら、この方法上での問題は、大変非常に単純化されるが、運動方程式の一般解を得ることは、未だに非常に困難である。しかし、幸運にも、核子周辺自己場、または、核子によるメソ粒子散乱を含む問題、に関する問題の議論は、そのような一般解なしで導き出される。これらの目的の為に、むしろ簡単な運動方程式の特殊解を知るだけで十分である。このようにして、これら簡単な問題の話を続ける。
===以後は省略===