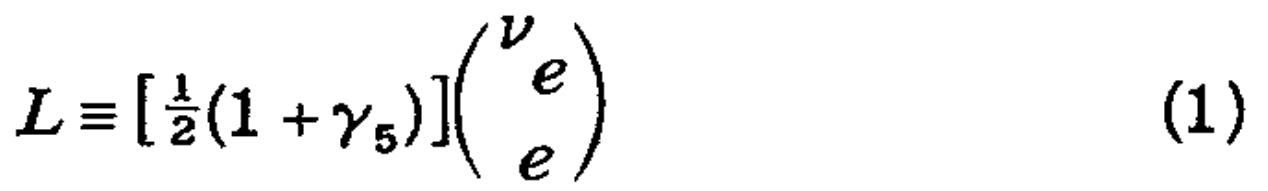
スティーブン・ウィンバーグの論文

レプトンのモデル

スティーブン・ウィンバーグ

核科学と物理部門研究所、マサチューセッツ工学研究所、ケンブリッジ、マサチューセッツ

（1967年10月17日受理）

　レプトンは光子と中間の多分弱い相互作用を介在するボソンとのみ相互作用する。何がこれら多重ゲージ場のスピン１ボゾン一式よりより自然であるだろう？この方法に立脚して、光子と中間メソンの質量とそれらの組み合わせ内で総合体は明白な違いである。弱い（力）と電磁気相互作用が関係する対称性を想像することによるこれらの違いはラグラジアンの正確な対称性であり、真空により破壊されるものではないことを理解することを望めるだろう。しかしながら、これは望まれない質量がないゴールドストンボゾン（理論が自発的対称性の破れを起こしたときに生じる質量ゼロのボゾン粒子） の状況を起こさせる。この文章は、突然壊れる電磁気と弱い相互作用間の対称性と、しかし、そこでゲージ場としての光子と中間ボゾン場を導入することによりゴールドストンボゾンは無効かされることを記述する。

そのモデルは再普通化が可能であろう。

　我々の試みを観測されるただ相互に電子的レプトンに接続された対称性グループに対し制限するだろう－例えば、ミューオン的レプトン、別の非観測レプトン、ハドロンなどである。その対称性はそれから左巻きの2重線である。

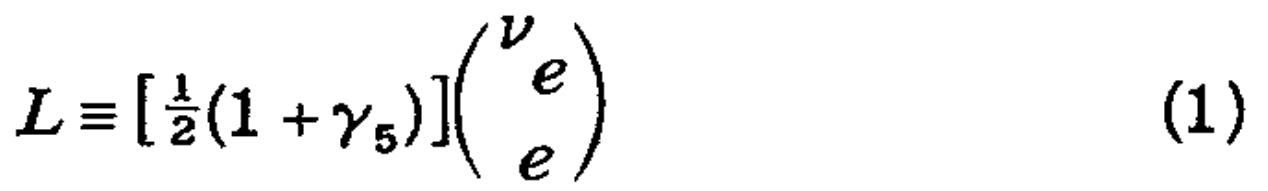
それと右巻きの単重線である。

最大のグループは不変なＬ上で振る舞う電子アイソスピンＴを基礎とする力学的項で、左右巻きの電子的レプトン数Ｎ「Ｌ」、Ｎ「Ｒ」を加えるラグラジアン

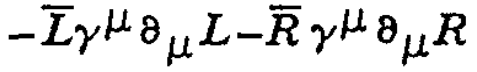
から離れる。

我々が知る限り、これらの二つの対称性は完全に破壊されない：

電荷

と電子数

について。

　それゆえ、ＴとＹと組みのＡ「μ」とＢ「μ」のゲージ場を加え、０スピンでＴとＹを破壊し、電子に質量を与えるだろう例外的真空値2重線を加えるラグラジアンＬとＲを構築できるのである。

ただＴとＹゲージ遷移下で不変な再普通化可能なラグラジアンは

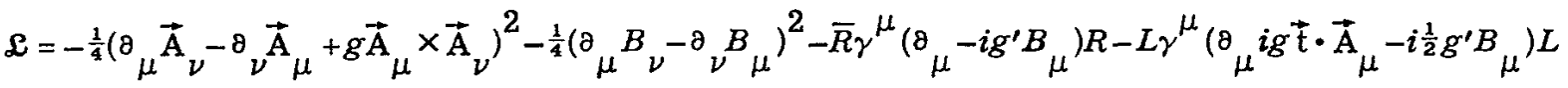
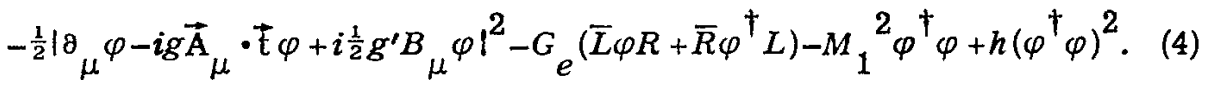
となる。

Ｇ「e」を実現するＲ場の状況を選ばなければならなかったし、また真空例外値λ≡＜φ0＞を実現するＬとＱ場の状況を調整することができる。物理的φ場はそれゆえ、φｰと

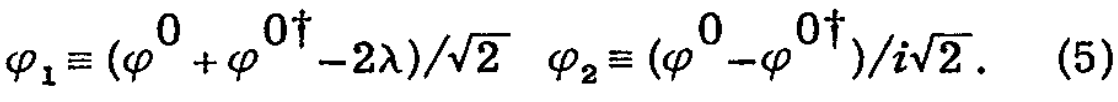
である。

=== 以下同様な式と文章が続くのみなので省略 ===