湯川秀樹の論文
On the Interaction of Elementary Particles
(素粒子の相互作用)
湯川 秀樹
(1935年受取)
(( 省略 ))
電磁場スカラーポテンシャルとの類似性として、関数は、中性子と陽子間の場を記述する為に導入された。この関数は、電磁ポテンシャルの波動関数に類似した方程式を満足する。
ここで、方程式は
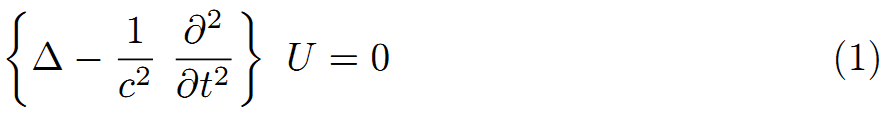
(1)式は、ただ中心対称(1/r)の、乗法及び加法の定数を除いて、固定解を持つ。
しかしながら、中性子と陽子間のポテンシャル力はクーロン力形式ではない、しかし、さらに急速に減衰する。例えば、それは次式で表現される。

“g”は、電荷の次元を持つ定数であり、“e”は[cm^(3/2)・(/Sec・gr^(1/2))]を“λ”は[1/cm]の次元を持つ。この関数は、中心対称波動方程式として、固定であるから、
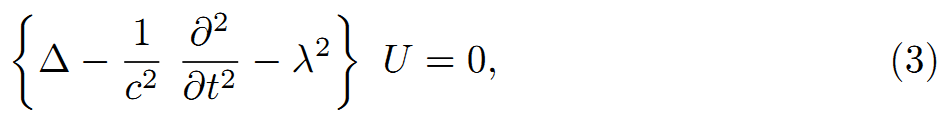
この方程式を、真空中のUの正しい方程式と仮定してみよう。
核子存在下、U場は、それらと相互作用し、中性子から陽子への遷移の原因となる。ここで、次の行列を導入する。
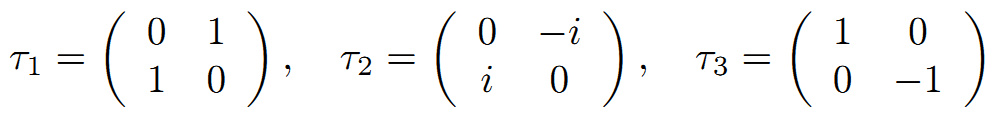
中性子と陽子状態を、それぞれτ3=1とτ3=-1と表し、波動方程式を次式で与える。
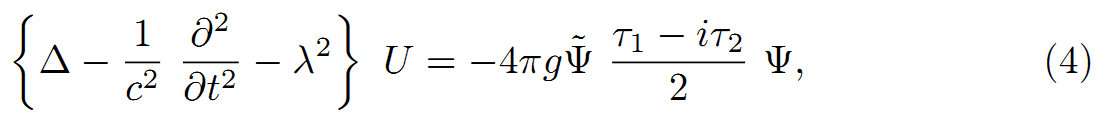
Ψは核子の波動関数を示す、これは、位置、1か-1の値をとるτ’スピン及び
時間の関数である。次に、次式をみたす複素共役関数U^(x,y,z)、
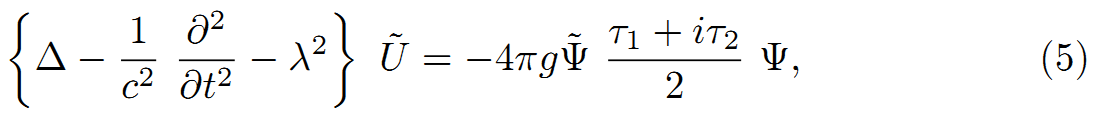
は導入され、陽子から中性子への逆遷移に一致する。類似方程式は、電磁場のベクトル・ポテンシャルに類似したベクトル関数を保持する。
しかし、我々は、ひととき、核子の正しい相対性理論がないことを無視する。それ故に、スピンを無視した簡単な非相対論的波動方程式は核子に使用され、次式の方法となる。
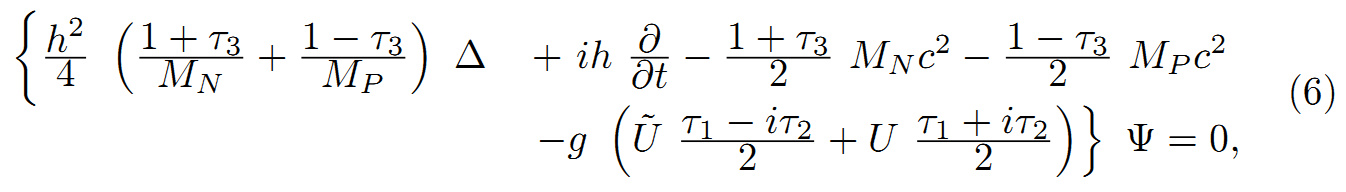
h<h~の間違いだろう>はプランク定数で2πで割ったものであり、M[N]、M[P]はそれぞれ、中性子と陽子の質量である。gの前にマイナス記号を付けた理由は後で言及される。
式(6)は次式のハミルトニアンに一致する。

P「→」は粒子の運動量である。もし、M[N]c^2-M[P]c^2=DとM[N]+M[P]=2Mと置いたなら、式(7)は近似的に、次式となる。
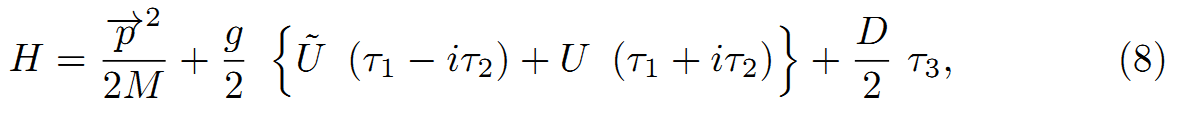
定数項MC2は省略した。
ここで、2つの核子をそれぞれ、点(x1,y1,z1)と点(x2,y2,z2)とし、それらの相対速度は小さいと仮定する。点(x2,y2,z2)の核子に対する点(x1,y1,z1)の場は、式(4)と式(5)から、次式となる。
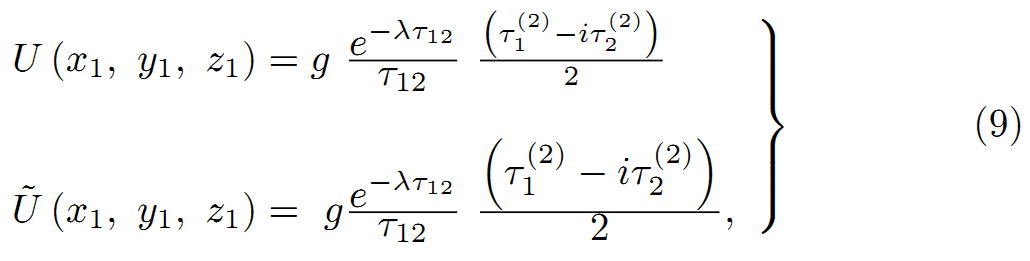
![]()
は、それぞれ、第一核子と第2核子に関連した行列であり、τ12はそれらの距離である。
こうして、外部場がない場合、その機構のハミルトニアンは次式で与えられる。
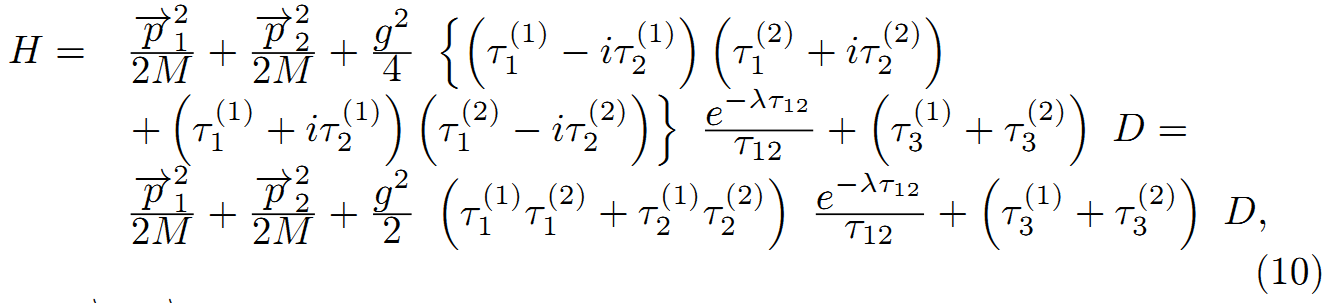
P1「→」、P2「→」は核子の運動量である。
もし“Platzwecheselint” 整数を採用したなら、このハミルトニアンはハイゼンベルグのハミルトニアンと同等である。

中性子間相互作用を除いて、陽子間の静電場反発は重要と見られない。ハイゼンベルグはJ(r)に正符号を使用した、そして、H「2」の最低エネルギー状態のスピンは0だった、従って、このケースでは、g^2の前の負符号に起因して、実験から要求されるのだが、最低エネルギー状態はスピン1である。
方程式に現れる二つの定数gとλは実験による比較から決定される。
例えば、核子にハミルトニアン(10)を使用した場合、H「2」の質量欠損を計算することができる。陽子のよる中性子の散乱確率により、相対速度が光速に比較して小さいことがわかった。
荒い評価で、もしλの値の範囲を10^12[cm^-1] から10^13[cm^-1]とするならば、実験結果と一致する計算された値が示せる。それと、gは、ときどき、基本チャージeである。しかしながら、熟考しても、gとe間の直接的関係は示唆されない。
熟考されたU場は一般的な量子理論により、量子化されるだろう。
中性子と陽子は双方ともフェルミ統計に従い、U場に従う量子はボーズ統計に従うべきであり、量子化は電磁場の類似事象として、実行可能だろう。
電荷の保存法則は、量子は電荷として、+eか-eを持たなければならないことを要求する。場の量(子)(数)Uは、負のチャージ数を増加させる操作子であり、各自それぞれに、正にチャージした量子の数を減らす。
Uの複素共役U「~」は逆操作子である。
次に、示す。
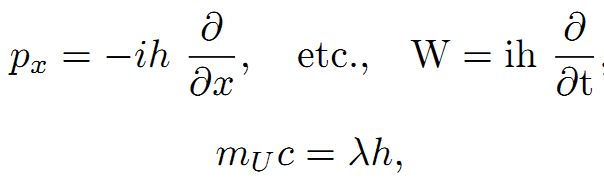
自由空間のUの波動方程式は、次式で記述される。
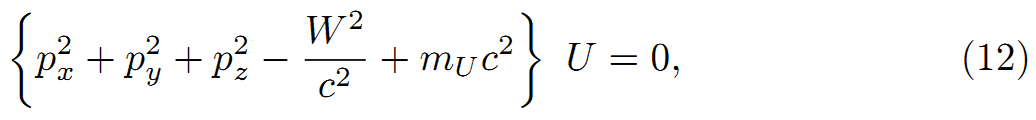
場に従う量子は固有質量m[U]=λh/cを持つ。
λ=5×10^12[cm^-1]と仮定すると、m[U]の値として、電子質量の200倍を得る。
このような正か負のチャージ(電荷?)と大きな質量を持つ量子は、実験では見つけられていない。上記の理論は、間違った線上にあるように見える。
しかし、普通の核子遷移変換について、そのような量子は外宇宙へ放出可能ではないだろう。<< OUTER 外の:OUR 私達の:間違い? >>
例えば、熟考してみると、エネルギーの中性子状態W[N]からエネルギーの陽子状態W[P]への遷移について、それらは、各自の固有エネルギーを含む。
それらの状態は次の波動関数で表現される。
中性子:
![]()
陽子:
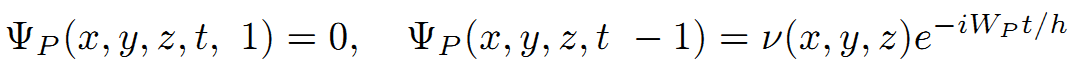
(4)式の右側の式は、
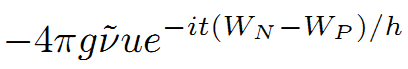
と現れる。
U=U‘(x、y、z)Exp(iωt)と置くと、次式を得る。
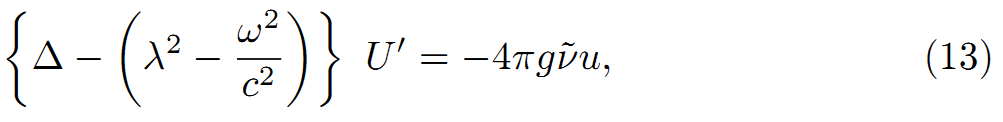
ω=(W[N] -W[P])/hを統合すると、次の解を得る。
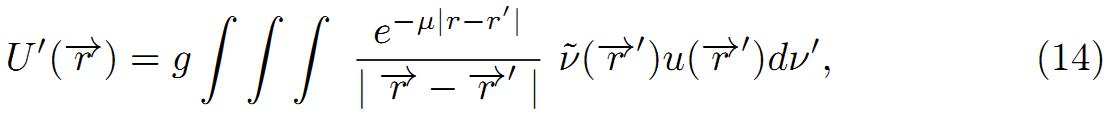
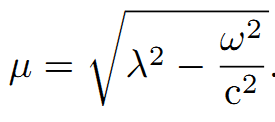
もしも、λ>|ω|/c か m[U]c^2>| W[N] -W[P]|ならば、μは実数で、関数J(r)は、式-g^2・(Exp(-μr)/r)を持つハイゼンベルグ(関数?、行列?)であり、μの中で、しかしながら、| W[N] -W[P]|に依存し、小さく、より小さくなり結局、m[U]c^2に近づく。これは、| W[N] -W[P]|が増えるに従い、中性子と陽子間相互作用の範囲が増加することを意味する。
<< J(r)は、ν(r)かu(r)か何かの間違いか?>>
ここで、核子による中性子の(弾性、非弾性)散乱は、次の二つの過程の結果と
考えることが可能である。:核子と陽子中で、中性子が陽子状態に移る過程と、後者は、陽子が正力学エネルギーの中性子状態への飛躍過程であり、合計エネルギーはそれらの過程を通して保存される。討論を越えて、これらは、散乱確率は、いくつかのケースで中性子の速度を増加させるだろうことを見い出せる。
“Bonner”の実験から、中性子の衝突断面積は増加し、実際に、鉛のケースでは、速度と共に増加する、ところが、炭素と酸素のケースでは、それは、減ることとなり、減少率は後者より前者がより遅い。この効果の起源は明らかではない、しかし、熟考すると、少なくとも、それに反論する。
もし、核子内の陽子の結合エネルギーがm[U]c^2と比較可能となるならば、
前者の中性子相互作用の範囲は、中性子の速度に従って、かなり増加する。このケースで、酸素のケース-すなわち自由陽子-より、より遅く断面積は減少する。いま、C「12」とB「11」の質量差から見積もられるC「12」中の陽子の結合エネルギーを次式とする、
![]()
これは、質量単位-電子質量の30倍-中の結合エネルギー0,0152に一致する。こうして、炭素のケースで“Bonner”に観測された効果を期待することができる。この議論は、ただ仮説的であり、別の説明はあるが、もちろん実施されていない。
次に、もしも、λ<|ω|/c か m[U]c^2<| W[N] -W[P]|ならば、μは純虚数となり、Uは球状の非減衰波で、m[U]c^2より大きいエネルギーの-外(我々の?)宇宙に、規定された中性から陽子への核子遷移により、放出可能な-量子を含む。
電子波のケースでは、U波の速度は、光速cより大きいが、群速度はより小さい。
このような重たい量子が、もし、それらが常に存在していて、なぜ、未だに発見されていないかの理由は、質量m[U]はとても大きく、条件m[U]c^2<| W[N] -W[P]|は、通常の核子遷移では、満たされていない事実の為と考えられる。
ここまでは、ただ核子との相互作用U量子のみを考えた。ここから、我々の理論に従ってみよう、核子が中性から陽子へ転換するとき、放出された量子は、エネルギーの吸収結果、正エネルギーの電子状態に対する負エネルギーニュートリノ状態により起こされる光子で吸収されうるだろう。こうして、反ニュートリノと電子は、同時に核子から放出される。このような核量子の干渉は、基本的に核子の直接結合の過程により計算されたβ崩壊の固有事象ではない、そして、ちょうど光子は、γ線の内部保存理論により、陽子干渉に最終結果として影響しない。それゆえ、この理論は基本的にフェルミ理論とは異なる。
フェルミは、電子とニュートリノは放射性の核から同時に放出されると考えた、しかし、これは公式に、光子は負エネルギーニュートリノから正エネルギーの電子状態へ飛び移ったとする仮定と同等である。
もし、電子とニュートリノのアイゲン(Eigen)関数が、それぞれΨk、Φk、k=1,2,3、4、…とすると次式となる。<< Eigen:生物物理学者、(Eigen)関数=??? >>

この式は、式(5)のU「~」の右側に加えられるべきものであり、g’はgと同じ次元を持つ新しい定数である。
ここで、ニュートリノ状態のエネルギーと運動量に関するアイゲン(Eigen)関数は、ちょうど、これらφ’k=-σ[klφ~l]により与えられるφkと反対の位置にあり、反対にφk=-σ[klφ~l’]で、σは次式となる。
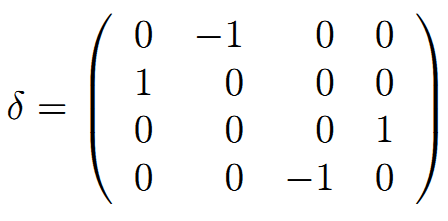
そして、(15)は次式となる。

式(13)と(15)から、核子の相互作用エネルギーを得た、そして光子の表式は
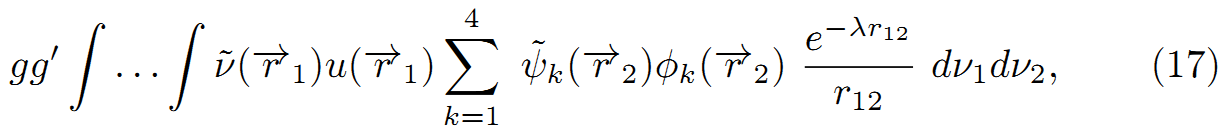
(これは、)次の二つの過程である:核子は、アイゲン関数u(r)のニュートリノからアイゲン関数v(r)の陽子状態へ落ち、同時に、光子は負エネルギーφk(r)のニュートリノから、正エネルギーψk(r)の電子へ飛び移る。式(17)のλはμの代わりである、β線のエネルギー範囲の上限合計と等しい、中性子と陽子状態のエネルギーの差から、電子とニュートリノの固有エネルギーは常にm[U]c^2と比較して小さい。
λは、電子とニュートリノ状態の波数より、とても大きく、関数Exp(-λr12)/ r12は近似的にx2、y2、z2に関する統合である4π/λ^2が掛けられたσ関数と考えられる。
要素4π/λ^2は次式から来る。
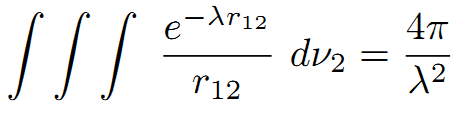
こうして、(17)は次式となる。
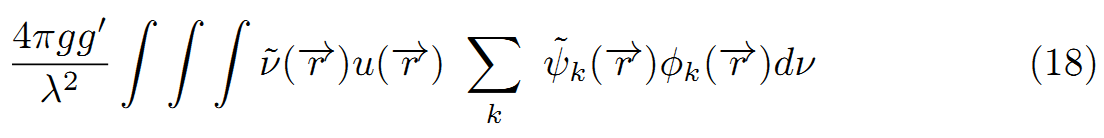
または、(16)により
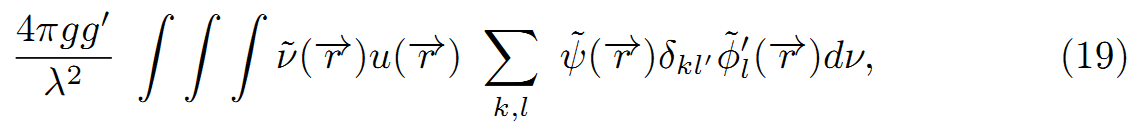
フェルミのgの代わりとして係数4πgg’/λ^2を除いて、φ’k(r)と ψk(r)の正エネルギー状態ニュートリノと電子の放出により、フェルミの表現(21)と同じである。
これは、ニュートリノと電子の相互作用は、中性子と陽子の場合より小さく、ニュートリノは中性子より、非常に強く貫通性を持ち、それゆえ観測は困難である。gとg’の違いは、たぶん重い粒子と軽い粒子の質量の違いのよるのだろう。
基本粒子の相互作用は、ボーズ統計に従い、固有質量と元素チャージを持つ仮定の量子を熟考することにより記述される。中性子と陽子の大きい相互作用はβ崩壊と同じ位小さい確立なので、このような重粒子量子相互作用は軽粒子の場合より、はるかに重要である。
もし、これらが常に存在して、十分に吸収され、物質に近く接近するならば、これら量子はチャージとエネルギーを後で放出するだろう。それから、もし、負チャージの量子が過剰に放出されるならば、粒子は負のポテンシャルでチャージされている。