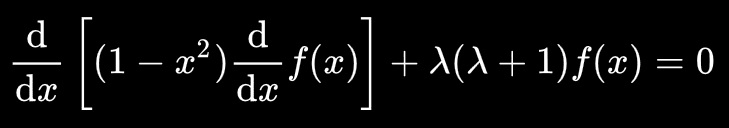
量子力学 シュレディンガー方程式
この資料は150冊以上の量子力学の書籍と100以上のWEB資料を参照し作成された。
この資料では量子力学の一般的な主張や共通な主張に対して解説をしている。
あらゆる資料から図などは1点も、物理式などは1行も転載はしていない、従って著作権侵害は完全にない。
量子力学は110年間に25万から30万の論文が提出されたといわれる。 シュレディンガー方程式が正しい前提で、これを応用した概念や用語が300以上存在するといわれる。 量子力学の論文や参考書を30万冊読んでも決して理解できない。 ではどうすれば良いか、物理学の基礎的根源次元の知識を使用してシュレディンガー方程が何であるかを正しく理解すれば良い。
線形微分方程式を解く問題において
f(x)=∑[n=0~∞]C[n]X^nとおき元の微分方程式に代入して解く方法。
例:f<i>+3f'+5f-4=0
級数表現のf<i>とf'を計算し元の式に代入し、x^n,x^(n-1)…でまとめる。常に右辺と同じ0になる条件としてc[n]で作られた係数が0と等しいとおき,c[n]とc[n-1]の関係などから数列を特定する。この方法は必ず有効な訳ではない。
有効な条件は
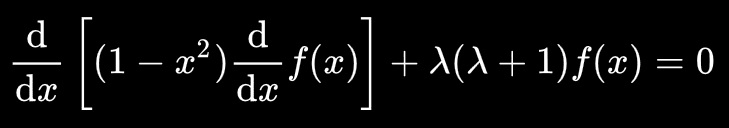
微分積分300年の歴史で発見された級数解法で解ける非線形微分方程式の一つ。
留意点:
この方程式は一切の変更は受け付けない、少しでも変更すると級数解法では解けなくなる。
例:式の一部を理由なく変更する。
例:Z=xcos(x)とおき問題を解き最後までZのままで終える。
(xcos(x))^2=4でZ^2=4とおき解をZ=2と主張する。
例:Z=rcos(θ)とおき、後でZ=2rとおく。
例:Z=rcos(θ)とおき、後でZ=2rとおく。変数を元の戻すときにZ=2rを使用する。
この例では変数θをcos(θ)として不正に消している。
この方法は究極的に強烈で、この方法を繰り返し適用すれば変数の数を自由に減らすことが可能であり、任意の関数の形を別の任意の形に自由自在に変更可能となる。
最終結果も自由自在に決定することができる。
量子力学の根源的重要事項である。
こちらを参照せよ。
式で表現しようとする対象が明確に定義されており、既に存在するものか、存在しない場合は再現が可能であること。
物理変数は有効な物理的実在に対する物理量である必要がある。
物理式は有効な物理変数で表現しようとする物理学的対象の状態とその変化を適切に表現する必要がある。
物理量は全て観測や実験により特定可能である必要がある。ただし、観測を切り離した物理式の場合はその必要がない。
式の全ての物理変数は有効な物理的実在に対する有効な物理量であると確認できる。
物理学的対象の表現したい部分の状態を適切に表現ができている。
物理学的対象の表現したい部分の変化を適切に表現ができている。
上記の事項が実験により確認される。
一つの陽子と一つの電子から構成される最も簡単な原子。
普通原子に分類され、普通原子同士で電子ペアを形成し共有結合する。
電子が陽子に極めて近い範囲で拘束されている。具体的な電子の運動は全く理解されていない。
マクスウェル方程式から加速する電子は電磁波を放出するはずだが、なぜか放出しない。
水素原子の単独状態ではラジカルという状態で水素マイナス・イオンと比較して100倍以上反応性が高いことが実験により確認されている。
化学の本や資料で”水素”という言葉が使われた場合、分子に関する文脈では結合した水素原子を示し、水素を分離したとか抽出したなどの文脈の場合は水素分子(2分子水素)を示す場合が多い。
水素原子2個が結合してできる分子。
各水素原子の電子が原子核(陽子)の中間位置で電子ペアを形成し安定した分子となる。
水素分子が二つに分裂する場合通常は陽子と水素マイナスイオンとに分離する。
ラジカル原子やラジカル分子との反応で一時的にラジカル水素ができる可能性は十分あると考えられる。
水素の原子核(陽子)に中性子が一つ結合しており、質量が約2倍である。
単独分離された水素原子は極めて短時間しか存在できない。
水素原子を単独分離して安定に容器に保存するなどは不可能である。
もし、金属容器に水素原子を入れても一瞬で電子を金属に取られて陽子になるか、逆に電子を得て水素マイナスイオンとなる。
もし、有機物で構成される容器に入れても一瞬で化学反応が起こり、ラジカル状態が存在しない状態に移行する。
プラズマ核融合炉に関する資料で水素を複雑な磁場で閉じ込めるとの資料があるがプラズマ状態は原子を原子核と電子に分離した状態で水素原子を分離したわけではない。
水素原子の単独分離は100年前も現在も、そして100年後も不可能である。
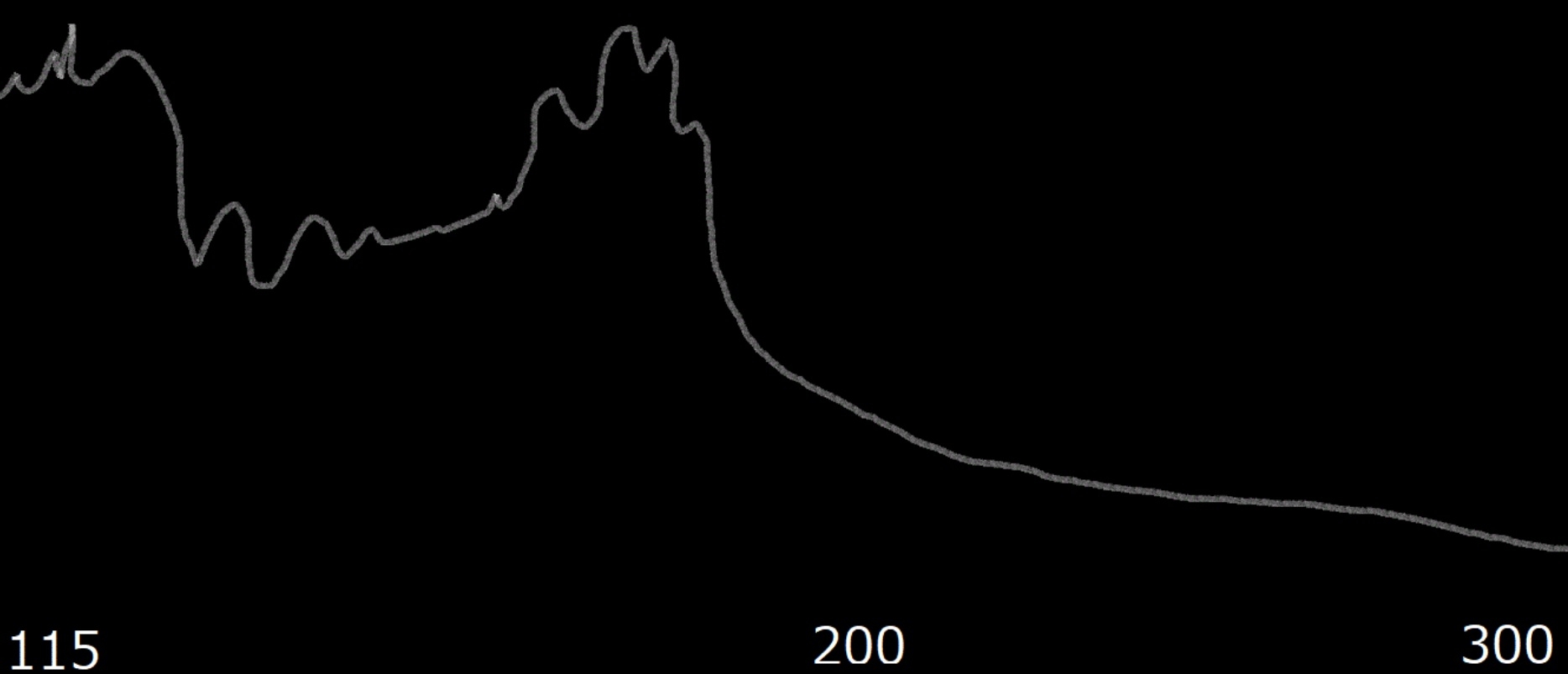
重水素ガス・ランプはガラス管に重水素分子が封入されたランプである。
重水素ランプ光の周波数強度分布は120[nm]~400[nm]で連続的に分布し、120nm]と160[nm]付近にピークがあるようだ。
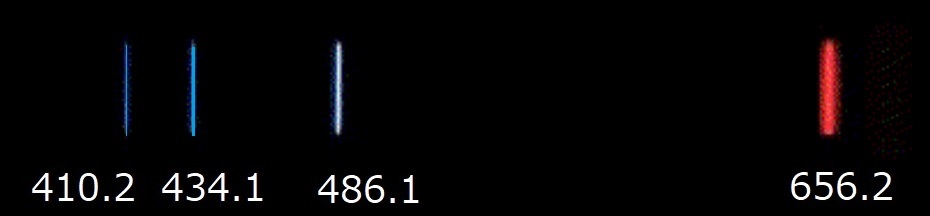
水素分子ガス・ランプのピーク部分の図 (波長[nm])
解説にはH(水素)とあるがH2(水素分子)を封入したランプである。水素ランプ光の周波数強度分布は180[nm]~400[nm]で連続的に分布し、656[nm]、486[nm],434[nm]、極弱く410[nm]付近にピークがあるようだ。

不活性ガスのNe(ネオン原子)を封入したランプである。
ネオン・ランプ光の周波数強度分布は570[nm]~750[nm]の範囲に、20か所位のピークがあるようだ。

液体金属の水銀を封入したランプである。
水銀・ランプ光の周波数強度分布は250[nm]~800[nm]の範囲に、10か所位のピークがあるようだ。
結局、原子、分子ガスに高圧電流を流すと連続発光し物質毎に特有な光のスペクトルを示すのかは全く未知である。
資料は「PDF Lambの実験 水素」で入手してください。
タングステン・チューブに大電流を流しそこに水素分子ガスH2を流し水素原子Hに分離し、さらに電子銃で電子を当てて水素原子の励起状態を生成する実験との主張である。
化学の知識がないと、何となく正しい主張と考えるかもしれないが、水素Hを単独分離は絶対に不可能である。
熱したチューブに水素分子ガスを通しても、僅かしか熱はガスに伝わらない。
H+とH-に分離するかも疑わしいし、仮に分離しても直ぐにH2分子に戻る。
HラジカルとHラジカルに分離するとは、さらに疑わしい。仮に分離しても直ぐにH2分子に戻る。
Hラジカルが分離して、もし直ぐにH2分子に戻らなければ、空気中に2割程度含まれるO2分子と燃焼反応してH2O水分子ができるだろう。
実験資料を見てもHラジカルが分離に成功したとは到底考えられない。
当然、H水素原子(=水素ラジカル)の励起状態などは全く確認できない。
理論物理学ではこの情報が、H水素原子(=水素ラジカル)の励起状態が存在することの証拠とされている。
「分子や原子を封入したランプ光のスペクトル」で述べた通りガス・ランプについては全て未知である。
そもそも、なぜ発光するのか自体が理解されていない。
周波数強度分布もなぜそうなるかは理解されていない。
各物質毎に複数あるピーク点についても、なぜそうなるかは理解されていない。
ラジカル開裂が起こっている証拠は存在しない。
ラジカル開裂が起こり、さらにH水素原子(=水素ラジカル)が励起状態になることは全く確認されていない。
H水素原子(=水素ラジカル)の励起状態が存在する証拠は存在しない以上、H水素原子の励起状態は存在しないと考えるべきである。
唯一厳密に解けるとされる水素原子の例を考える。
暫くは、水素原子(陽子一つと電子一つを考える。)
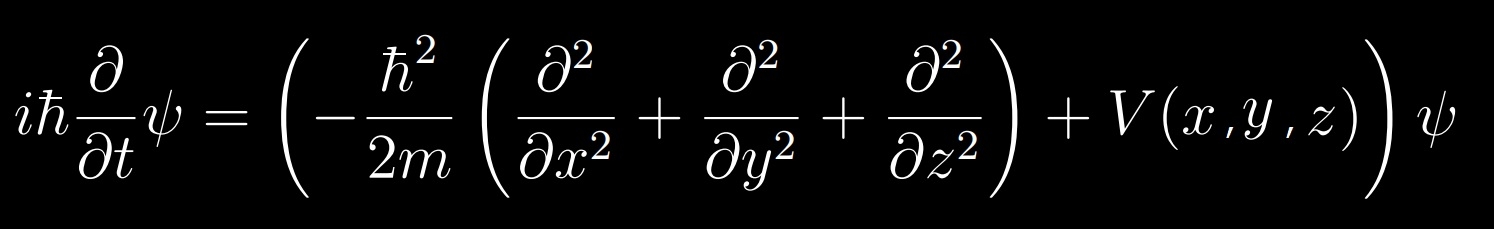
h[バー]は定数、i
は虚数単位、mは対象電子の質量か、V(x,y,z)は時間に依存しない対象全体のポテンシャル・エネルギーとされる。
Φ(x,y,z,t)は波動関数と呼ばれ、|Φ|^2は存在確率密度とされる。
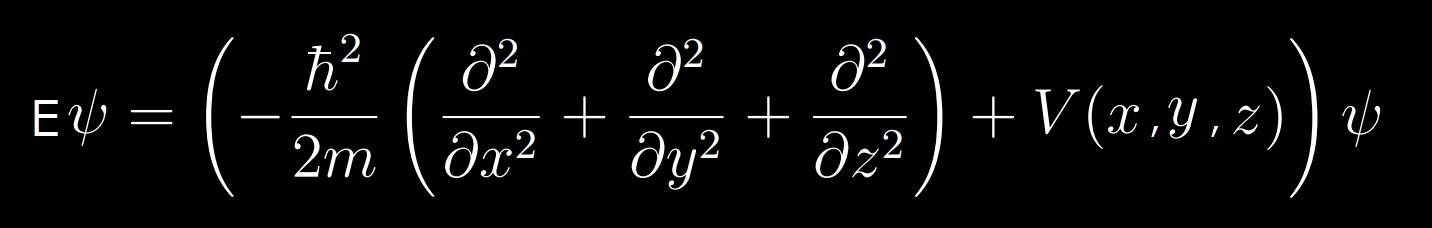
Eは対象全体のエネルギーとされる。
例えば、下の図のような実験を考える。
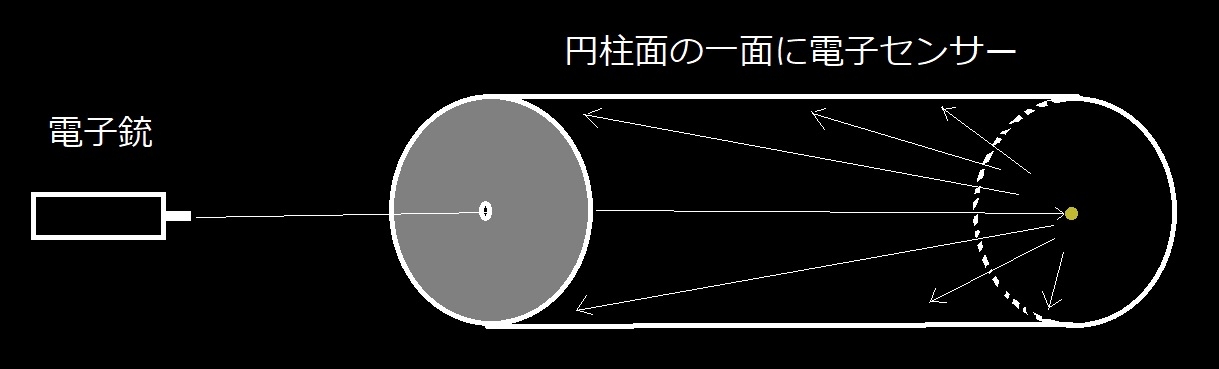
円柱の底の中心に試料が設置してあり、電子銃から電子が1個ずつ発射される。円柱面には一面にセンサーが設置しており、電子がどの位置に到着したか特定できる。到着した位置から試料で反射した電子の反射角度を決定できる。また反射角毎に電子が反射した確率が定義でき、実験によりその確率を特定できる。
重要な点:
観測対象は何か。
この実験における観測とは何か定義されていること。
観測対象が何をもって”観測された”とするか定義されていること。
この実験における確率とは何か定義されていること。
100分率確率の合計は1(100%)となること。
上記事項が実験により再現と確認が可能であること。
シュレディンガー方程式の一般式は物理式として有効かどうか検証してみる。
3[kg]+5[m]=8[m/s]
が無条件で絶対に正しくないことは小学生でも理解できるし、また理解すべき事項である。
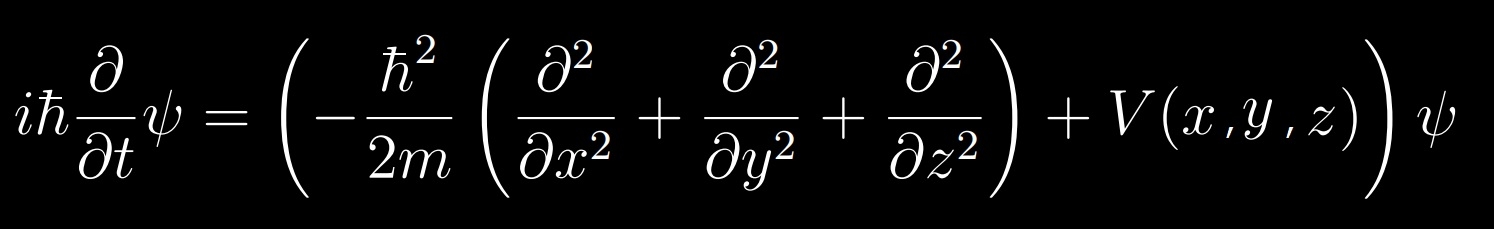
左辺は [φ/s]
右辺第一項は [φ/kg/s2]
右辺第二項は [φNm]
となるのでこの式は無条件で(全ての物理法則の)全宇宙において完全に物理式としては不正であり、物理学的な意味を持たない記号の羅列となる。
(これで理解し納得したならば、以後は読み飛ばし可能である。)
式で表現しようとする対象が明確に定義されており、既に存在するものか、存在しない場合は再現が可能であること。
シュレディンガー方程式は水素原子のみ唯一式が解けるとしているので水素原子を考える。水素原子は確かに存在する、しかし水素原子はラジカル原子であり単独分離は不可能であり再現できない。
物理変数は有効な物理的実在に対する物理量である必要がある。
波動関数と呼ばれるΦはこの条件を満たしていない。
物理式は有効な物理変数で表現しようとする物理学的対象の状態とその変化を適切に表現する必要がある。
この式は物理学的対象の状態を表現できていない。
仮に波動関数Φが確定しても、これが物理学的対象の状態を表していない、なぜなら核や電子の位置を表すことができないからである。
この式は物理学的対象の状態の変化を表現できていない。
理由は同様である。
物理量は全て観測や実験により特定可能である必要がある。ただし、観測を切り離した物理式の場合はその必要がない。
シュレディンガー方程式は明らかに積極的に観測行為を関係させているが、原子核や電子の位置とその移動を実験により特定できない。
確率密度なるものも全く定義されていない。
何をもって確率密度の観測に成功したのか定義されていない。
単独分離した原子や分子から電子に関する何らかの確率情報を得ることは不可能である。
式の全ての物理変数は有効な物理的実在に対する有効な物理量であると確認できる。
波動関数Φはこの条件を満たしていない。
物理学的対象の表現したい部分の状態を適切に表現ができている。
そもそも何を表現したいのか明確ではなく、この式はこの条件を満たしていない。
物理学的対象の表現したい部分の変化を適切に表現ができている。
そもそも何を表現したいのか明確ではない。
波動関数Φの時間微分が物理学的対象の時間変化を適切に表現できる可能性はない。
上記の事項が実験により確認される。
実験により式の検証はされたことが110年に渡り1度もない。なぜなら、この式は物理学式としては完全に無効であり、物理学的対象に対応させることが不可能である。
観測対象は何か。
観測対象は明らかには定義されていない。従ってこの条件を満たしていない。
この実験における観測とは何か定義されていること。
観測とは何か定義されていない。
観測対象が何をもって”観測された”とするか定義されていること。
観測対象が何をもって”観測された”とするか定義されていない。
この実験における確率とは何か定義されていること。
確率とは何か定義されていない。
100分率確率の合計は1(100%)となること。
確率とは何か定義されていないので論外である。
上記事項が実験により再現と確認が可能であること。
物理式として有効でないので、実験による再現も確認も不可能である。
物理式が正常で有効である為には全ての条件を完全に満たす必要がある。ところが、シュレディンガー方程式の一般式は一つとして条件を満たしていない。従って、シュレディンガー方程式は正常な物理式ではない。
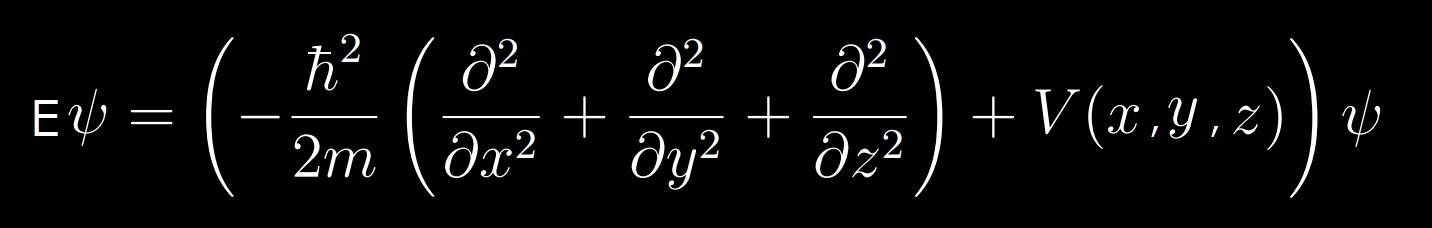
この式の物理単位を調べる。
左辺は [φ・Nm]
右辺第一項は [φ/Kg/s2]
右辺第二項は [φ・Nm]
となるのでこの式は(全ての物理法則の)全宇宙において完全に物理式としては不正であり、物理学的な意味を持たない記号の羅列となる。
(これで理解し納得したならば、以後は読み飛ばし可能である。)
省略
物理式が正常で有効である為には全ての条件を完全に満たす必要がある。ところが、時間に依存しないシュレディンガー方程式は一つとして条件を満たしていない。従って、時間に依存しないシュレディンガー方程式は正常な物理式ではない。
物理学は物理対象(物質と物理場)の時間変化を扱う学問であり、物理式に時間が直接または間接にも含まれないのは物理学としても物理式としても正常ではない。水素原子内の電子の様子は未知であるが少なくともある部分でマクスウェル方程式に従い運動変化(時間変化)し続けているだろう。
補足:
難解に見せかけるためシュレディンガー方程式の一般式ではi (虚数単位)が式にあったが、時間に依存しないシュレディンガー方程式では時間微分とi が消えてかわりにE(対象全体のエネルギー)が導入されるが、なぜこのようになるのか正常な説明が存在しない。
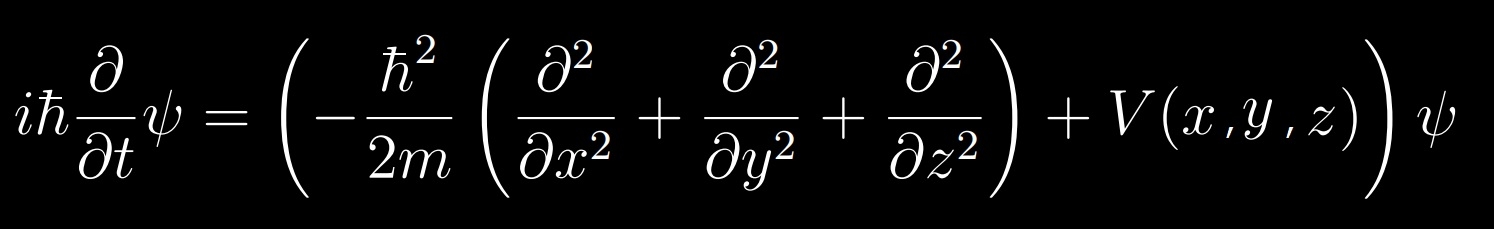
rはr(x,y,z)でx,y,zに関する関数である。
x,y,zの3変数に関する非線形2階微分方程式であり、とても解けるとは考えられない。
当然、この式の解が求まる求まないに関わらず、この式は正常な物理式ではない。
「水素原子のシュレディンガー方程式の解法」を150冊以上の参考書と100以上のWEB資料で確認をした。
ほとんどの資料では結果のみを記述している。
計算の途中経過を少しでも記述しているのは極僅かである。
計算を詳細に記述した資料は一つか二つしか見つけられない。
詳細に記述された資料を検証してみる。
先ず、この式を直交座標x, y, zの関数から球座標r, θ, Φ の関数に変換して考えるとしている。
直交座標x, y, zから球座標r, θ, Φ への変換式:
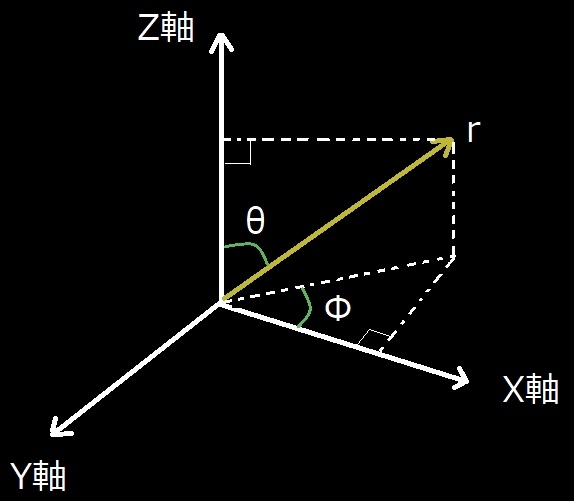
x=r SinθCosΦ
y=r SinθSinΦ
z=r Cosθ
合成関数の偏微分の公式を使用し計算を続けるとされる。
ーーー計算の途中省略ーーー
ある程度計算が進むと
数学的不正が続出することになる。
水素原子のシュレディンガー方程式は正常な物理式ではない。
水素原子のシュレディンガー方程式は絶対に解けない。
「水素原子のシュレディンガー方程式」の章でのべた通り、
シュレディンガー方程式は正常な物理式ではない。
唯一解けるとされる水素のシュレディンガー方程式は絶対に解けない。
時間を直接も間接的にも含まず物理場を含め全て時間変化しないというのは物理学ではない。
唯一解けるとされる水素のシュレディンガー方程式は絶対に解けないので、当然にEが確定することはない。
ただ単に嘘、作り話、デタラメである。
理論物理学者の主張では量子力学とシュレディンガー方程式の適用範囲は原子、分子、それらと電子の相互作用まで及ぶとしている。
水素原子のシュレディンガー方程式が解けたとして、確定した波動関数Φのどこが水素原子を表現しているのだろうか?
原子を再現できるとしているが、理論物理学者公認で水素原子のシュレディンガー方程式しか解けないということになっているのに酸素原子や窒素原子の電子ペアや共有電子、共有結合などを、どう表現できているというのだろうか?
シュレディンガー方程式には共有電子のスピンやラジカル性などを表現する要素などないのに表現できているというのはありえないことである。
分子を表現できるとしているが、例えば最も単純な2水素分子を再現するには陽子を含めた4体問題として扱う必要があるが、水素原子の電子一つまともに表現できない状態であり、分子を表現できるはずはない。
シュレディンガー方程式と量子力学は数学的物理学的に意味のない文字や記号の羅列ということになる。
シュレディンガー方程式(=波動関数)を応用、発展させた300以上の用語と概念は全て数学的物理学的に意味のない文字や記号の羅列ということになる。