式(1)
E=MC^2について
多くの論文が光子に質量概念を適用し運動量保存則とエネルギー保存則から光子エネルギーE=mC^2やE=(1/2)mC^2やE=(2/3)mC^2などとする多くの論文が出された。
内容は省略する。
(100%正しくないので論文を説明しても意味がない。)
「物体の慣性は、その物体に含まれるエネルギーに依存するか」
ベルン、1905年
私が研究の基礎においたのが、マクスウェルーヘルツの方程式と相対性原理である。この基礎によって私が導いた結果の内、次のものが特に重要である。
光の平面波からなる系が、座標系(x,y,z)から見たときにエネルギーlを持ち、光線の進行方向はx軸と角度φをなすものとする。座標系(x,y,z)に対してx軸方向に速度vで移動する座標系を座標系(x’,y’,z’)とする。
このとき光の集団エネルギーは座標系(x’,y’,z’)で測定すると
式(1)
となる。
座標系(x,y,z)で静止している物体があり、座標系(x,y,z)で見た場合のエネルギーをE0とし、座標系(x’,y’,z’)で見たものをH0とする。
その物体が、x軸と角度φをなす方向に、エネルギーL/2の光平面波を放出し、同時に反対方向に同量の光平面波を放出したとする。この間にこの物質は静止しエネルギーの原理を満たさなければならない。
このエネルギーを座標(x,y,z)で測定してE1、座標系(x’,y’,z’)で測定してH1とする。
このとき式(1)を使用して、次の式が得られる。
二つの式を引き算すると
式(4)
差H-Eは付加的な定数Dを除いて座標系(x’,y’,z’)で見たときの運動エネルギーKである。Dは光が放出される過程で変化しないので、次のように記述できる。
H0-E0=K0+D
H1-E1=K1+D 式(5)
こうして
式(6)
を得る。
座標系(x’,y’,z’)で測定した運動エネルギーは光を放出した為に減少する。
さらに差K0ーK1は電子の運動エネルギーと同じ形で物体の速度に依存する。
4次以上の量を無視すると
K0-K1=(1/2)(Lv^2)/(C^2) 式(7)
を得る。
この式から直ちに次の結論を得る。
物体が、エネルギーLを光の放射で放出すると、その物体の質量はL/C^2だけ減少する。
つまり、エネルギー L=mC^2 となる。
もしも、この理論が事実と合えば、(光の)放射は放出した物体から(光を)吸収した物体へと慣性を運ぶことになる。
マクスウェルーヘルツの方程式(=マクスウェル方程式)は1行も出てこない。
相対性原理の主張は全ての慣性系で物理法則は同じように記述されるであり、この論文の主張と真逆である。
光の平面波”とは何か未定義。
”光の平面波”を特定など不可能である。
全ての座標系で物理法則は同じ形で記述されるという相対性原理と矛盾する主張である。
式(1)は何の根拠もないデタラメである。
自身の主張の相対性原理と矛盾する。
対象から光子群が対称をなして放出されるので、対象は全ての観測系からみて慣性運動を続けるはずである。
対象から光子群が放出されることにより対象内部構成分子原子の平均運動エネルギーの低下すなわち温度の低下が起こるのみである。
対象は慣性運動を続ける、すなわち速度は変化しない。
対象は慣性運動を続ける。
何のことか理解できない。
そのような事実はない。
根拠もデタラメである。
慣性の概念を理解していない。
根拠のない全てデタラメである。
全てデタラメであり正常な主張が1行もない。
複数の特殊相対論の論文で”E=MC^2”が導出されている。我々が調査では5~10通り位の導出の種類が見つかった。
概要としては、静止系と運動系について、対称の運動量やエネルギーがどの様に見えるか考える。
運動系で、ローレンツ変換式を適用した相対論的運動エネルギーや相対論的運動量の式を導入する。
結果として質量mのエネルギーがE=mC2であるとの主張がなされる。
この資料で述べた通りローレンツ変換は正常な物理学とは完全に関係がない。
ローレンツ変換を適用した物理式は数学的物理学的に意味がない文字や記号の羅列でしかない。
「観測と物理学」で述べた通り観測者ごとに観測対象は異なって観測されるが事実は常に一つであり、このことからE=mC2との結論が求められることはない。
水素分子:H2、酸素分子:O2、H2O:水
H2X2とO2ー>H2O の反応は爆発反応となり、多くの光を発し運動エネルギーが上昇する。
H2 2個とO2が1個が独立して存在するより、 H2Oが1個の状態の方が安定状態である。
逆に水H2Oを酸素と水素に分解するには電気分解などエネルギーを加える必要がある。
反応の前後で物質は増えも減りもしない。これは化学の基本である。
原子核は陽子と中性子で構成され、原子核の陽子数ごとに最も安定する中性子数が存在する。
中性子は原子核内では安定するが、単独では安定せず1時間以内で陽子と電子に崩壊する。
ウラン235は核は幾つかのより小さい原子核に分裂し中性子も放出する。
複数の分裂形式がある内の1例を考える。
ウラン235->セシウム137とルビジウム95(+ヘリウム+陽子)+中性子+エネルギーを放出
ルビジウム95ー>モリブデン95+中性子+エネルギーを放出
この反応の前後で陽子と中性子数の合計は変わらない、つまり反応の前後で物質は増えも減りもしない。
水素を小型原子爆弾の爆発により瞬間的に高密度高温に超圧縮することにより水素核融合を起こす核爆弾である。
この反応の前後で陽子と中性子数の合計は変わらない、つまり反応の前後で物質は増えも減りもしない。
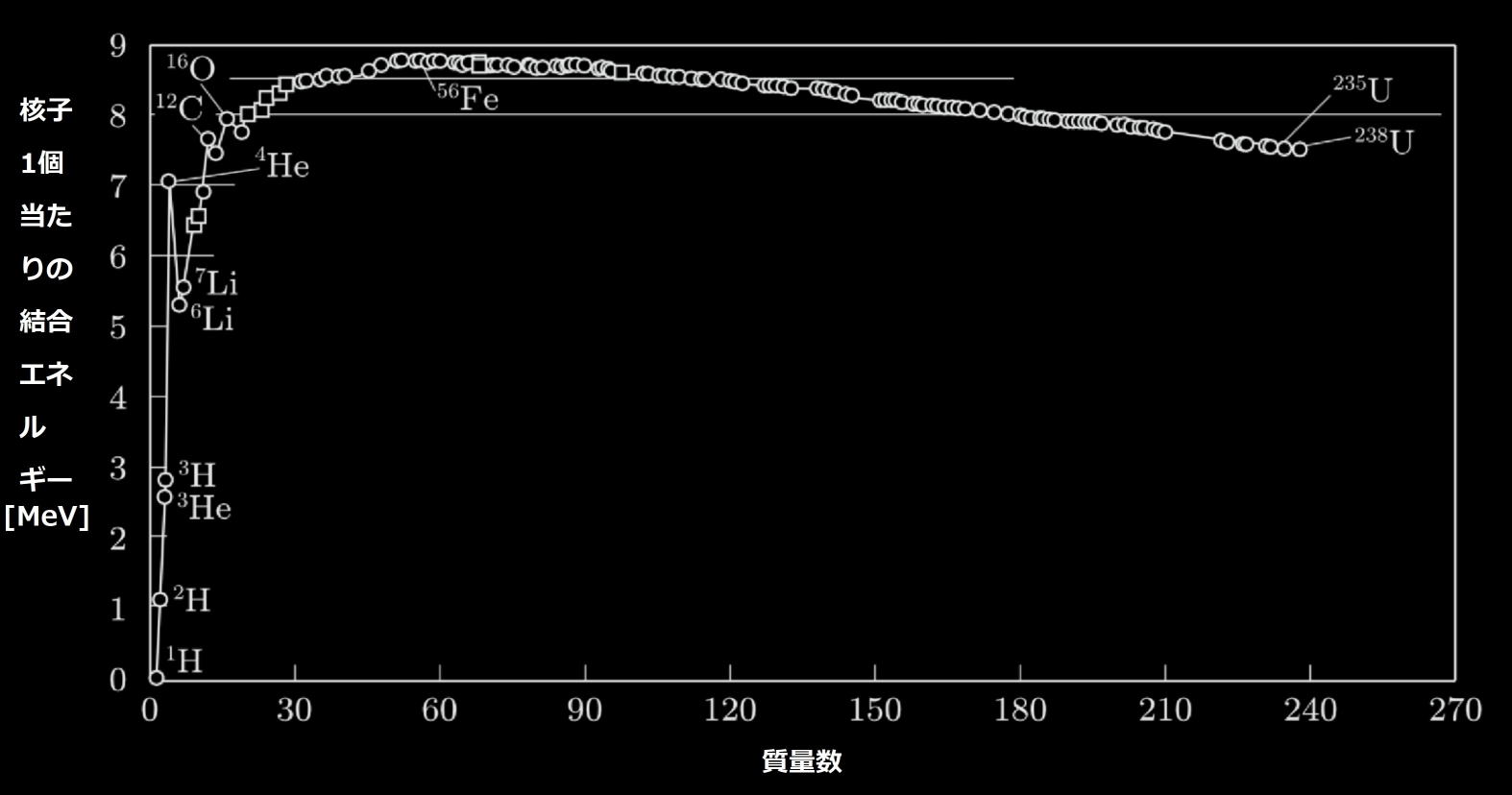
重力と比較すると電磁気力は10^38倍であり、強い力はさらに約100倍程度と予想される。
普通原子の結合距離は100~200[pm]である。一方原子核内の核子間の平均の距離 は約2[fm] と予想されている。
( 1[pm]=10^-12[m]、 1[fm]=10^-15[m] )
核力と化学結合力の比率は距離の効果が(100[pm])^2/(2[fm] )^2で2.50*10^9で力が100倍なので合計2.50*10^11となる。さらに核分裂では複数個に分裂し、さらに何度か分裂を繰り返す。この効果を平均で6倍と仮定する。
全て合計して核反応では、化学反応に比較して質量当たり1500億倍の莫大なエネルギーが放出されるのである。
東京都でダイナマイト1本分の核分裂爆発でエネルギーが放出されると計算すると、1[m^2]の面積にダイナマイト68本分のエネルギーが放出されるという計算結果になった。これは広島型原爆と比較しても上回る規模であろう。
E=MC2のC2は莫大のイメージと合い、まるで本当の様に感じさせる。
しかし、質量mは物質(陽子、中性子、電子)の物理場と相互作用したときの加速しずらさを表す物質特有の不変物理量であり、物質の存在量を表わす物理量ではない。
また、物質が消滅したり生成するという事実は存在しない。つまり、質量がエネルギーに変換するという主張は2重にデタラメである。
質量は物質の加速しずらさを表す各物質特有の不変物理量であり、理論物理学者の質量mを物質の存在量とする扱いは完全に正しくない。
物質が消滅する事実は存在しない。
当然、物質がエネルギーに変換するというのは嘘、作り話である。