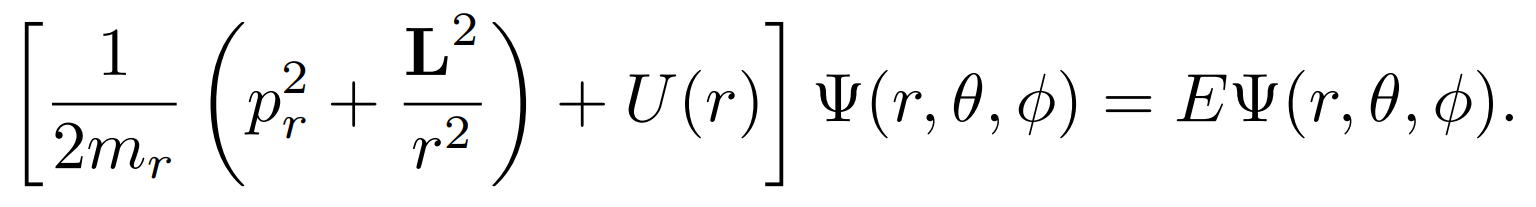
巻末練習
橋本 幸士 氏
「宇宙のすべてを支配する数式」
S=∫ d4x√(ーdetGμν(x))[ (1/16πGN) (R[Gμν(x)] ーΔ)ー(1/4)Σ[i=1~4]tr(Fμν(i)(x))+Σ[f]ψー(f)(x)iΦψ(f)(x)+Σ[g,h](yghΦ(x)ψ(g)(x)+h.c.)+|DμΦ(x)|2ーV[Φ(x)] ]
この数式は「素粒子の標準模型の作用」に「アインシュタイン=ヒルベルトの作用」を加えたもので、現時点で宇宙のほとんど全ての現象を記述できる数式なのである。
正常な物理学者が見れば一瞬から数秒で出鱈目と判別が可能な式であるが、初学者が練習するには丁度良いだろう。
物理式の背景の解説
どのような状況の何を考えているか解説が全くない。
物理式中の文字の説明
文字や記号が変数か未知関数か解説が全くない、さらに文字や記号が何の物理量に対応しているか説明がない。
式が正常な物理式で構成されているか否か
一目で正常な物理式でないと判断できる。
次元解析(物理単位解析)ー次元の統一性の確認:
右辺は9項あるが、全て完全に次元(物理単位)は異なりそろわない。
次元解析(物理単位解析)ー有効な次元か確認:
右辺は9項あるが、全て完全に次元(物理単位)は正常ではない。
式の詳細内容が存在するか確認
例えばGμνは4X4=16の要素を持つ行列であるが、各要素の説明がなく実際には意味がない記号である。
式の詳細内容を確定可能か確認
∫ d4x:後の式をx,y,z,tについて積分をする意味だがそのような複雑な積分は不可能である。
Gμν、R、Δ、tr、Fμν、Φ、ψ、Dμなど全て内容が未定義で確定は当然不可能である。
この式は間違いなく世界唯一独自式であるが発見や発明としての証明は存在しない。
完全パーフェクトに出鱈目である。
小学校低学年の子供でも1時間位訓練すれば作成可能な数学的物理学的に意味のない文字や記号の羅列である。
村山 斉氏
PDFファイル:タイトル:Future Experimental Program
「高エネルギー からの必然的な影響」
高エネルギー物理の効果はほとんど抑制力により消される。
L=LSM+(1/Δ)L5+(1/Δ^2)L6
しかし、高エネルギー物理が記憶する二つの用語が存在する。
LSM=ー(1/g2)F2μν+ψーiDψ+DμH+DμH-yψーψH+(θ/64π2)FF~ーλ(H+H)2+μ2 H+HーΛCC
(ここまで全文を転載)
正常な物理学者が見れば一瞬から数秒で出鱈目と判別が可能な式であるが、初学者が練習するには丁度良いだろう。
物理式の背景の解説
どのような状況の何を考えているか解説が全くない。
物理式中の文字の説明
文字や記号が変数か未知関数か解説が全くない、さらに文字や記号が何の物理量に対応しているか説明がない。
式が正常な物理式で構成されているか否か
一目で正常な物理式でないと判断できる。
次元解析(物理単位解析)ー次元の統一性の確認:
右辺は7項あるが、全て完全に次元(物理単位)は異なりそろわない。
特に1項目F2μνは4X4の行列であり,他は一つの量で完全に正常ではない。
次元解析(物理単位解析)ー有効な次元か確認:
右辺は7項あるが、全て完全に次元(物理単位)は正常ではない。
式の詳細内容が存在するか確認
例えばDμは四つの要素を持つ行列であるが、各要素の説明がなく実際には何の意味もない記号である。
式の詳細内容を確定可能か確認
全ての記号が説明がなく確定不可能である。
Gμν、R、Δ、tr、Fμν、Φ、ψ、Dμなど全て内容が未定義で確定は当然不可能である。
相対論や量子力学の概念や記号が含まれるか確認
この式は間違いなく世界唯一独自式であるが発見や発明としての証明は存在しない。
完全パーフェクトに出鱈目である。
小学校低学年の子供でも1時間位訓練すれば作成可能な数学的物理学的に意味のない文字や記号の羅列である。
大栗 博司氏
PDFファイル:タイトル:
Symmetries in Quantum Field Theory and Quantum Gravity
(量子場の対称性と量子重力)
2.1 Splittability(分割性)
量子場の球対称性が続くとき、通常Gの随伴表現の保存流Jaμ方程式の存在一式と予想される対称集合Gは、リー集合として0以上の次元を持つことを意味する。ラグラジアン理論では、これは、この資料の定理[43,45]双方の結果ではないと思える。実際、一連の連続特定変数変換として連続対称性を定義する。
Φ’i(x)=Φi(x)+εafa,i(Φ(x)、∂Φ(x)、…)+O(ε2) (2.12)
この式は経路積分測度の結果を残す。
DΦ’eiS[Φ’]=DΦeiS[Φ] (2.13)
もし、いま、この集合を従属した位置に対するεaと協調させることを許すならば、その周辺で次式を得る。
DΦ’eiS[Φ’]=DΦ・Exp(iS[Φ] ーi∫ ddx√[-g]Jαμ ∂μεa+O(ε2) )
=DΦ・Exp(iS[Φ] +i∫ ddx√[-g]∇μJαμ ∂μεa+O(ε2) ) (2.14)
((以後省略))
173ページにわたり数学的物理学的に意味のない文字と記号の羅列に対して出鱈目な物理学風の解説をした大作である。
正常な物理学者が見れば一瞬から数秒で出鱈目と判別が可能な式であるが、初学者が練習するには丁度良いだろう。
物理式の背景の解説
どのような状況の何を考えているか解説が全くない。
物理式中の文字の説明
文字や記号が変数か未知関数か解説が全くない、さらに文字や記号が何の物理量に対応しているか説明がない。
式が正常な物理式で構成されているか否か
一目で正常な物理式でないと判断できる。
次元解析(物理単位解析)ー次元の統一性の確認:
どの項も、全て完全に次元(物理単位)は異なり単位はそろわない。
次元解析(物理単位解析)ー有効な次元か確認:
全て完全に次元(物理単位)は正常ではない。
式の詳細内容が存在するか確認
例えばJαμ はαXμ個の要素を持つ行列であるが、各要素の説明がなく実際には意味がない記号である。
式の詳細内容を確定可能か確認
多くの式が明らかに数学的形式が出鱈目であり、当然、式の詳細内容を確定は不可能である。
例:
(2.12)Φ’i(x)=Φi(x)+εafa,i(Φ(x)、∂Φ(x)、…)+O(ε2) について
Φi(x):波動関数Φがある以上量子力学に関する式となるので、添え字に虚数単位iは使用すべきでない。
∂Φ(x):∂は偏微分記号でこのような使われ方は不正である。
εaと ε2:ベクトル的な使われ方と普通の変数的な使われ方を同時にされている。
(2.13) DΦ’eiS[Φ’]=DΦeiS[Φ] について
未知変数か関数D、未知関数Φ、Φ’、S:当然式は何も決定できない出鱈目となる。
(2.14)DΦ’eiS[Φ’]=DΦ・Exp(iS[Φ] ーi∫ ddx√[-g]Jαμ ∂μεa+O(ε2) )
=DΦ・Exp(iS[Φ] +i∫ ddx√[-g]∇μJαμ ∂μεa+O(ε2) )について
全体構成:未知変数と未知関数が多数で絶対に何も確定できない出鱈目である。
∫ ddx:???
∂μ:∂は偏微分記号でこのような使われ方は不正である。
εaと ε2:ベクトル的な使われ方と普通の変数的な使われ方を同時にされている。
∇μ:∇の意味から、このような記述は不正である。
∇μJαμ
∂μεa:多くのことを無視しても、これだとベクトルになり他の非ベクトルと整合が取れない。
この式は間違いなく世界唯一独自式であるが発見や発明としての証明は存在しない。
完全パーフェクトに出鱈目である。
小学校高学年の子供でも1時間位訓練すれば作成可能な数学的物理学的に意味のない文字や記号の羅列である。
練習問題 - 4:
堀越 宗一(ホリコシ ムネカズ)氏
五神 誠(ゴノカミ マコト)氏
PDFファイル:タイトル:Cold Atom Quantum Simulator for Dilute Neutron Matter
(希薄な中性子物質に対する冷却原子量子シュミレータ)
希薄で低エネルギー条件では、フェルミオンは粒子より物質波として振る舞う。同じ質量mの二つの粒子が距離rで中心ポテンシャルU(r)で相互作用しているとして、それら相対運動はシュレディンガー方程式に従う一つの粒子の減少質量mr=m/2と考えることが可能である。
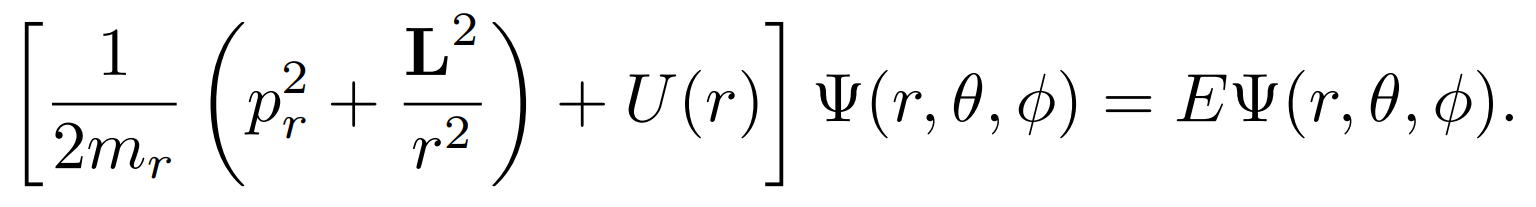
球対称のシュレディンガー方程式は次式で与えられる。
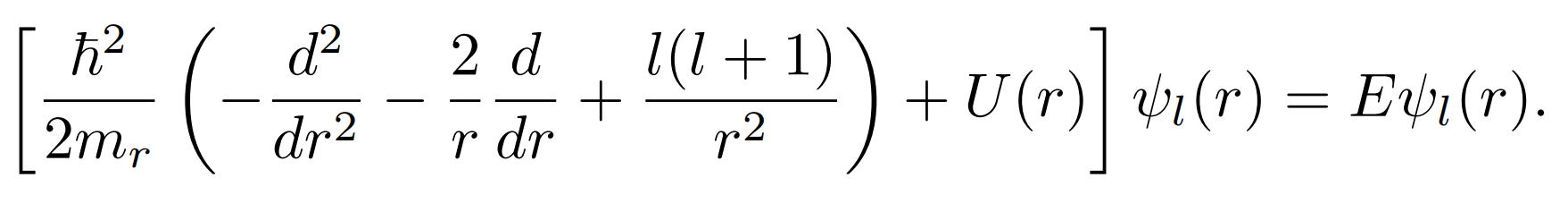
フェルミオンや物質波は物理学的に存在しない。
物理式の背景の解説
どのような状況の何を考えているか解説が全くない。
数学的形式はぎりぎり問題ない。
物理式中の文字の説明
文字や記号が変数か未知関数か解説がな全くない、さらに文字や記号が何の物理量に対応しているか説明がない。
式が正常な物理式で構成されているか否か
一目で正常な物理式でないと判断できる。
次元解析(物理単位解析)ー次元の統一性の確認:
どの項も、全て完全に次元(物理単位)は異なり単位はそろわない。
次元解析(物理単位解析)ー有効な次元か確認:
全て完全に次元(物理単位)は正常ではない。
式の詳細内容が存在するか確認
Lなど説明がなく式の概要もわからない。
式の詳細内容を確定可能か確認
U(r) 、Ψ(r、θ、φ)など未知関数は確定は不可能である。
この式は間違いなく世界唯一独自式であるが発見や発明としての証明は存在しない。
完全パーフェクトに出鱈目である。
小学校高学年の子供でも1時間位訓練すれば作成可能な数学的物理学的に意味のない文字や記号の羅列である。
これら論文の物理式と称する無意味な記号の羅列は小学生でも1時間位訓練すれば作成できるだろう。
記述部分は物理学的に正常な部分、まともな部分、正しい部分がどの論文も1行もないが小学生が数時間訓練すれば記述可能と言えばさすがに嘘になる。
しかし、物理学、化学、物性論の基礎的事項を理解している高校であれば物理分野テーマを一つに限定し数時間〜10時間程度の訓練で理論物理学の論文を(理論物理学者のように何の実験もしないで)作成可能となるだろう。